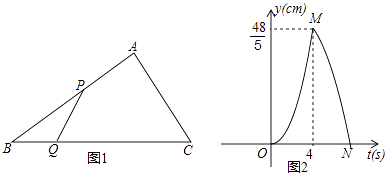题目内容
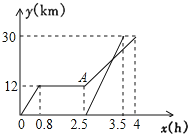
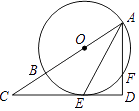
【题目】如图1,点A、B、C在坐标轴上,且A、B、C的坐标分别为![]() 、
、![]() 、
、![]() 过点A的直线AD与y轴正半轴交于点D,
过点A的直线AD与y轴正半轴交于点D,![]()
![]() 求直线AD和BC的解析式;
求直线AD和BC的解析式;
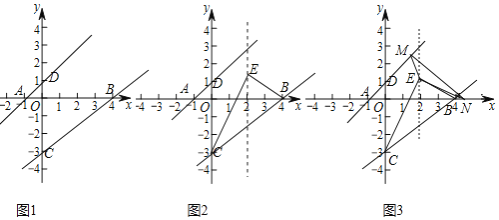
![]() 如图2,点E在直线
如图2,点E在直线![]() 上且在直线BC上方,当
上且在直线BC上方,当![]() 的面积为6时,求E点坐标;
的面积为6时,求E点坐标;
![]() 在
在![]() 的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当
的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当![]() 周长最小时,求
周长最小时,求![]() 周长的最小值.
周长的最小值.
【答案】![]() ,
,![]() ;
;![]() 点E的坐标为
点E的坐标为![]() ;
;![]() 周长的最小值
周长的最小值![]() .
.
【解析】
(1)∠DAB=45°,OA=DO=1,即点D的坐标为(0,1),将点A、D的坐标代入一次函数表达式,即可求解;
![]() 由
由![]() ,即可求解;
,即可求解;
(3)作点E关于直线AD对称点![]() ;找到点E关于x轴的对称点
;找到点E关于x轴的对称点![]() ,连接
,连接![]() 交AD于M点、交x轴于点N,则△MNE周长最小,即可求解.
交AD于M点、交x轴于点N,则△MNE周长最小,即可求解.
![]() ,
,
![]() ,即点D的坐标为
,即点D的坐标为![]() ,
,
将点A、D的坐标代入一次函数表达式:![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
则直线AD的表达式为:![]() ,
,
同理可得直线BC的表达式为:![]() ;
;
![]() 设直线
设直线![]() 与BC交于点F,点E坐标为
与BC交于点F,点E坐标为![]() ,则点F坐标为
,则点F坐标为![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
即点E的坐标为![]() ;
;
![]() 过点E点作
过点E点作![]() ,点E和
,点E和![]() 关于直线AD对称,
关于直线AD对称,
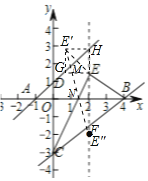
设直线![]() 与直线AD交于点
与直线AD交于点![]() ,连接
,连接![]() ,
,
找到点E关于x轴的对称点![]() ,
,
连接![]() 交AD于M点、交x轴于点N,此时,
交AD于M点、交x轴于点N,此时,![]() 周长最小,
周长最小,
![]() ,
,
![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则:![]() 周长的最小值
周长的最小值![]() .
.
故答案为:(1)y=x+1,y=![]() x-3;(2)点E的坐标为
x-3;(2)点E的坐标为![]() ;(3)△MNE周长的最小值
;(3)△MNE周长的最小值![]() .
.

练习册系列答案
相关题目
【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c |
|
|
3、4、5 | 2 | |
5、12、13 | 4 | |
8、15、17 | 6 |
(2)如果![]() ,观察上表猜想:
,观察上表猜想: ![]() (用含有m的代数式表示).
(用含有m的代数式表示).
(3)证明(2)中的结论.