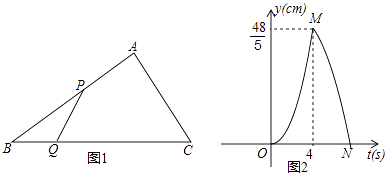题目内容
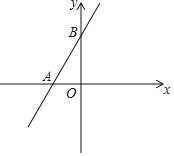
【题目】如图,抛物线y=ax2+ ![]() x+1(a≠0)与x轴交于A,B两点,其中点B坐标为(2,0).
x+1(a≠0)与x轴交于A,B两点,其中点B坐标为(2,0).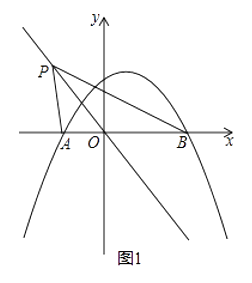
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=﹣x上的动点,当直线OP平分∠APB时,求点P的坐标;
(3)如图2,在(2)的条件下,点C是直线BP上方的抛物线上的一个动点,过点C作y轴的平行线,交直线BP于点D,点E在直线BP上,连结CE,以CD为腰的等腰△CDE的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.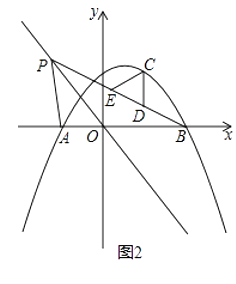
【答案】
(1)解:把B(2,0)代入y=ax2+ ![]() x+1,
x+1,
可得4a+1+1=0,解得a=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+1,
x+1,
令y=0,可得﹣ ![]() x2+
x2+ ![]() x+1=0,解得x=﹣1或x=2,
x+1=0,解得x=﹣1或x=2,
∴A点坐标为(﹣1,0)
(2)解:若y=﹣x平分∠APB,则∠APO=∠BPO,
如图1,若P点在x轴上方,PB与y轴交于点A′,
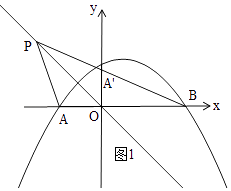
由于点P在直线y=﹣x上,可知∠POA=∠POA′=45°,
在△APO和△A′PO中 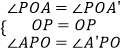 ,
,
∴△APO≌△A′PO(ASA),
∴AO=A′O=1,
∴A′(0,1),
设直线BP解析式为y=kx+b,
把B(2,0)、A′(0,1)两点坐标代入可得 ![]() ,解得
,解得 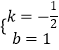 ,
,
∴直线BP解析式为y=﹣ ![]() x+1,
x+1,
联立 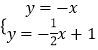 ,解得
,解得 ![]() ,
,
∴P点坐标为(﹣2,2);
若P点在x轴下方时,如图2,
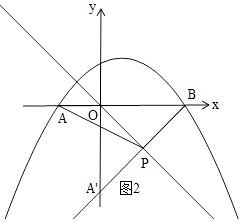
∠BPO≠∠APO,即此时没有满足条件的P点,
综上可知P点坐标为(﹣2,2)
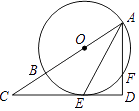
(3)解:存在,
如图3,作CH⊥PB于点H,
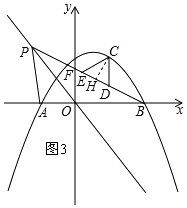
∵直线PB的解析式为y=﹣ ![]() x+1,
x+1,
∴F(0,1),
tan∠BFO= ![]() =
= ![]() =2,
=2,
∵CD∥y轴,
∴∠BFO=∠CDF,
tan∠CDF=tan∠BFO= ![]() =2,
=2,
∴CH=2DH,
设DH=t,则CH=2t,CD= ![]() t,
t,
∵△CDE是以CD为腰的等腰三角形,
∴分两种情况:
①若CD=DE时,则S△CDE= ![]() DECH=
DECH= ![]() t2t=
t2t= ![]() ,
,
②若CD=CE时,则ED=2DH=2t,
∴S△CDE= ![]() DECH=
DECH= ![]() 2t2t=2t2,
2t2t=2t2,
∵2t2< ![]() t2,
t2,
∴当CD=DE时△CDE的面积比CD=CE时大,
设C(x,﹣ ![]() x2+
x2+ ![]() x+1),则D(x,﹣
x+1),则D(x,﹣ ![]() x+1),
x+1),
∵C在直线PB的上方,
∴CD= ![]() =(﹣
=(﹣ ![]() x2+
x2+ ![]() x+1)﹣(﹣
x+1)﹣(﹣ ![]() x+1)=﹣
x+1)=﹣ ![]() =﹣
=﹣ ![]() ,
,
当x=1时,CD有最大值为 ![]() ,
,
即 ![]() t=
t= ![]() ,
,
t= ![]() ,
,
∴S△CDE= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
存在以CD为腰的等腰△CDE的面积有最大值,这个最大值是 ![]() .
.
【解析】(1)将点B坐标代入到抛物线的解析式可求得a的值,令y=0,得到关于x的方程,然后解关于x的一元二次方程即可;
(2)当点P在x轴上方时,连接BP交y轴于点A′,然后证明△APO≌△A′PO,依据全等三角形的性质可得到AO=A′O=1,从而可求得A′坐标,然后利用待定系数法可求得直线BP的解析式,联立直线y=-x,可求得P点坐标;当点P在x轴下方时,画图可知:∠BPO≠∠APO,即此时没有满足条件的P点;
(3)过C作CH⊥DE于点H,由直线BP的解析式可求得点F的坐标,结合条件可求得tan∠BFO和tan∠CDF,可分别用DH表示出CH和CD的长,分CD=DE和CD=CE两种情况,分别用t表示出△CDE的面积,再设出点C的坐标,利用二次函数的性质可求得△CDE的面积的最大值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
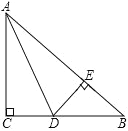
小学生10分钟应用题系列答案【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c |
|
|
3、4、5 | 2 | |
5、12、13 | 4 | |
8、15、17 | 6 |
(2)如果![]() ,观察上表猜想:
,观察上表猜想: ![]() (用含有m的代数式表示).
(用含有m的代数式表示).
(3)证明(2)中的结论.