题目内容
【题目】如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=﹣x+4(0≤x≤4),其中正确的是( )

A. ①②③B. ①②C. ①③D. ②③
【答案】A
【解析】
①正确.由AB∥CD,推出∠BAC+∠DCA=180°,由∠ACE=![]() ∠DCA,∠CAE=
∠DCA,∠CAE=![]() ∠BAC,即可推出∠ACE+∠CAE=
∠BAC,即可推出∠ACE+∠CAE=![]() (∠DCA+∠BAC)=90°,延长即可解决问题;
(∠DCA+∠BAC)=90°,延长即可解决问题;
②正确.首先证明AC=AK,再证明△QCE≌△PKE,即可解决问题;
③正确.只要证明AP+CQ=AC即可解决问题.
解:如图延长CE交AB于K.
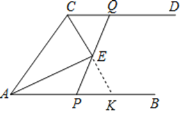
∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵∠ACE=![]() ∠DCA,∠CAE=
∠DCA,∠CAE=![]() ∠BAC,
∠BAC,
∴∠ACE+∠CAE=![]() (∠DCA+∠BAC)=90°,
(∠DCA+∠BAC)=90°,
∴∠AEC=90°,
∴AE⊥CK,△AEC是直角三角形,故①正确,
∵∠QCK=∠AKC=∠ACK,
∴AC=AK,
∵AE⊥CK,
∴CE=EK,
在△QCE和△PKE中,
 ,
,
∴△QCE≌△PKE,
∴CQ=PK,S△QCE=S△PEK,
∴S四边形APQC=S△ACK=2S△ACE,故②正确,
∵AP=x,CQ=y,AC=4,
∴AP+CQ=AP+PK=AK=AC,
∴x+y=4,
∴y=-x+4(0≤x≤4),故③正确,
故选:A.

 名校课堂系列答案
名校课堂系列答案【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c |
|
|
3、4、5 | 2 | |
5、12、13 | 4 | |
8、15、17 | 6 |
(2)如果![]() ,观察上表猜想:
,观察上表猜想: ![]() (用含有m的代数式表示).
(用含有m的代数式表示).
(3)证明(2)中的结论.