题目内容
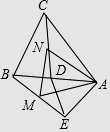
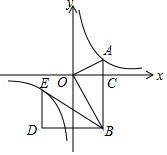
【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )

A. 120°B. 135°C. 145°D. 150°
【答案】D
【解析】
先判断出△ABC是等边三角形,根据等边三角形的每一个内角都是60°可得∠ABC=60°,再根据等腰三角形两底角相等表示出∠ADB、∠BDC,然后根据∠ADC=∠ADB+∠BDC求解即可.
∵AB=BC=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵AB=BC=BD,
∴∠ADB=![]() (180°∠ABD),
(180°∠ABD),
∠BDC=![]() (180°∠CBD),
(180°∠CBD),
∴∠ADC=∠ADB+∠BDC,
=![]() (180°∠ABD)+
(180°∠ABD)+![]() (180°∠CBD),
(180°∠CBD),
=![]() (180°+180°∠ABD∠CBD),
(180°+180°∠ABD∠CBD),
=![]() (360°∠ABC),
(360°∠ABC),
=180°![]() ×60°,
×60°,
=150°.
故选:D.

练习册系列答案
相关题目