题目内容
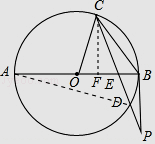
【题目】如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB. 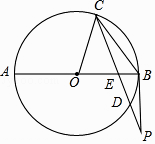
(1)求证:AEEB=CEED;
(2)若⊙O的半径为3,OE=2BE, ![]() =
= ![]() ,求tan∠OBC的值及DP的长.
,求tan∠OBC的值及DP的长.
【答案】
(1)证明:连接AD,
∵∠A=∠BCD,∠AED=∠CEB,
∴△AED∽△CEB,
∴ ![]() =
= ![]() ,
,
∴AEEB=CEED;
(2)解:∵⊙O的半径为3,
∴OA=OB=OC=3,
∵OE=2BE,
∴OE=2,BE=1,AE=5,
∵ ![]() =
= ![]() ,
,
∴设CE=9x,DE=5x,
∵AEEB=CEED,
∴5×1=9x5x,
解得:x1= ![]() ,x2=﹣
,x2=﹣ ![]() (不合题意舍去)
(不合题意舍去)
∴CE=9x=3,DE=5x= ![]() ,
,
过点C作CF⊥AB于F,

∵OC=CE=3,
∴OF=EF= ![]() OE=1,
OE=1,
∴BF=2,
在Rt△OCF中,
∵∠CFO=90°,
∴CF2+OF2=OC2,
∴CF=2 ![]() ,
,
在Rt△CFB中,
∵∠CFB=90°,
∴tan∠OBC= ![]() =
= ![]() =
= ![]() ,
,
∵CF⊥AB于F,
∴∠CFB=90°,
∵BP是⊙O的切线,AB是⊙O的直径,
∴∠EBP=90°,∴∠CFB=∠EBP,
在△CFE和△PBE中
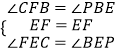 ,
,
∴△CFE≌△PBE(ASA),
∴EP=CE=3,
∴DP=EP﹣ED=3﹣ ![]() =
= ![]() .
.
【解析】(1)直接根据题意得出△AED∽△CEB,进而利用切线的性质的出答案;(2)利用已知得出EC,DE的长,再利用勾股定理得出CF的长,t即可得出an∠OBC的值,再利用全等三角形的判定与性质得出DP的长.
【考点精析】根据题目的已知条件,利用切线的性质定理和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是50
B.众数是51
C.方差是42
D.极差是21