题目内容
【题目】如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN. 下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE .
其中正确的结论是 . (填写所有正确结论的序号)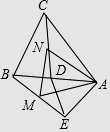
【答案】①②④
【解析】解:①在△ACD和△ABE中, ∵ 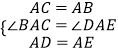 ,
,
∴△ACD≌△ABE(SAS),
所以①正确;②∵△ACD≌△ABE,
∴CD=BE,∠NCA=∠MBA,
又∵M,N分别为BE,CD的中点,
∴CN=BM,
在△ACN和△ABM中,
∵ 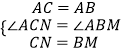 ,
,
∴△ACN≌△ABM,
∴AN=AM,∠CAN∠BAM,
∴∠BAC=∠MAN,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ABC∠AMN,
∴△ABC∽△AMN,
所以②正确;③∵AN=AM,
∴△AMN为等腰三角形,
所以③不正确;④∵△ACN≌△ABM,
∴S△ACN=S△ABM ,
∵点M、N分别是BE、CD的中点,
∴S△ACD=2S△ACN , S△ABE=2S△ABM ,
∴S△ACD=S△ABE ,
∵D是AB的中点,
∴S△ABC=2S△ACD=2S△ABE ,
所以④正确;
本题正确的结论有:①②④;
所以答案是:①②④.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是50
B.众数是51
C.方差是42
D.极差是21