Question

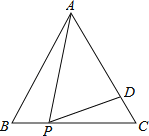
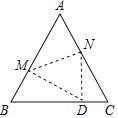
【题目】如图，在等边△ABC中，把△ABC沿直线MN翻折，点A落在线段BC上的D点位置（D不与B、C重合），设∠AMN＝α．

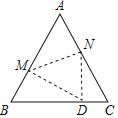
（1）用含α的代数式表示∠MDB和∠NDC，并确定的α取值范围；

（2）若α＝45°，求BD：DC的值；

（3）求证：AMCN＝ANBD．

Answer 1

【答案】（1）∠MDB＝＝2α﹣60°，∠NDC＝180°﹣2α，（30°＜α＜90°）；（2）+1；（3）见解析

【解析】

（1）利用翻折不变性，三角形内角和定理求解即可解决问题．

（2）设BM＝x．解直角三角形用x表示BD，CD即可解决问题．

（3）证明△BDM∽△CND，推出＝，推出DMCN＝DNBD可得结论．

（1）由翻折的性质可知∠AMN＝∠DMN＝α，

∵∠AMB＝∠B+∠MDB，∠B＝60°，

∴∠MDB＝2α﹣60°，∠NDC＝180°﹣∠MDB﹣∠MDN＝180°﹣（2α﹣60°）﹣60°＝180°﹣2α，（30°＜α＜90°）

（2）设BM＝x．

∵α＝45°，

∴∠AMD＝90°，

∴∠BMD＝90°，

∵∠B＝60°，

∴∠BDM＝30°，

∴BD＝2x，DN＝BDcos30°＝x，

∴MA＝MD＝x，

∴BC＝AB＝x+x，

∴CD＝BC﹣BD＝x﹣x，

∴BD：CD＝2x：（x﹣x）＝+1．

（3）∵∠BDN＝∠BDM+∠MDN＝∠C+∠DNC，∠MDN＝∠A＝∠C＝60°，

∴∠BDM＝∠DNC，

∵∠B＝∠C，

∴△BDM∽△CND，

∴＝，

∴DMCN＝DNBD，

∵DM＝AM，ND＝AN，

∴AMCN＝ANBD．