��Ŀ����
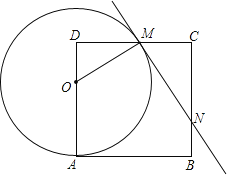
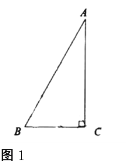
����Ŀ����ĩ��С����С��������ѧ����ѧ֪ʶ��������ǰС�ӵĿ�������ʱ������ѡ���˺Ӷ��ߵ�һ�ô���������ײ���Ϊ��A�����������ڵİ���ѡ���˵�B��ʹ��AB��Ӱ���ֱ������B��������BC������AB���ӳ�����ѡ���D������DE��ʹ�õ�E���C��A���ߣ�
��֪��CB��AD��ED��AD�����BC��1m��DE��1.5m��BD��8.5m������ʾ��ͼ��ͼ��ʾ���������ز�����Ϣ����ӿ�AB��
���𰸡��ӿ�Ϊ17�ף�
��������
��������֤��ABC��ADE���ٸ������������εĶ�Ӧ�߳ɱ����������AB�ij�.
��CB��AD��ED��AD��
���CBA����EDA��90�㣬
�ߡ�CAB����EAD��
��ABC��ADE��
��![]() ��
��
�֡�AD=AB+BD��BD=8.5��BC��1��DE��1.5��
��![]() ��
��
��AB��17��
���ӿ�Ϊ17�ף�

 �Ķ��쳵ϵ�д�
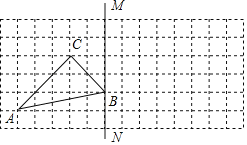
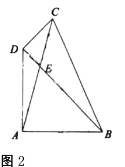
�Ķ��쳵ϵ�д�����Ŀ����1����![]() �У�
��![]() ��
��![]() ����ͼ1����
����ͼ1����![]() ��
��![]() ��������������ϵ����֤����Ľ��ۣ�
��������������ϵ����֤����Ľ��ۣ�
��2��ͼ2�����ı���![]() �У�
�У�![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
����
����Ŀ���۲��±���
x | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 |
y=x2��2x��2 | ��1.79 | ��1.56 | ��1.31 | ��1.04 | ��0.75 | ��0.44 | ��0.11 | 0.24 | 0.61 |
��һԪ���η���x2��2x��2=0�ھ�ȷ��0.1ʱһ�����Ƹ��ǡ�________�������������ߵĶԳ��ԣ�����֪�÷��̵���һ�����Ƹ���________����