题目内容
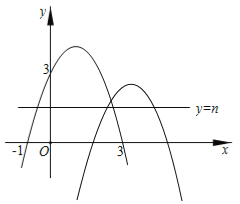
【题目】如图，已知二次函数G1：y＝ax2+bx+c（a≠0）的图象过点（﹣1，0）和（0，3），对称轴为直线x＝1．
（1）求二次函数G1的解析式；
（2）当﹣1＜x＜2时，求函数G1中y的取值范围；
（3）将G1先向右平移3个单位，再向下平移2个单位，得到新二次函数G2，则函数G2的解析式是 ．
（4）当直线y＝n与G1、G2的图象共有4个公共点时，直接写出n的取值范围．
【答案】（1）二次函数G1的解析式为y＝﹣x2+2x+3；（2）0＜y≤4；（3）y＝﹣（x﹣4）2+2；（4）n的取值范围为
＜n＜2或n＜．
【解析】
（1）由待定系数法可得根据题意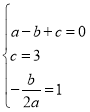得
解得
，则G1的解析式为y＝﹣x2+2x+3;(2)将解析式化为顶点式，即y＝﹣（x﹣1）2+4，当x＝﹣1时，y＝0；x＝2时，y＝3；而抛物线的顶点坐标为（1，4），且开口向下，所以当﹣1＜x＜2时，0＜y≤4；（3）G1先向右平移3个单位，再向下平移2个单位，得到新二次函数G2，则函数G2的解析式是y＝﹣（x﹣1﹣3）2+4﹣2，即y＝﹣（x﹣4）2+2，故答案为y＝﹣（x﹣4）2+2；（4）解﹣（x﹣4）2+2═﹣（x﹣1）2+4得x＝
，代入y＝﹣（x﹣1）2+4求得y＝，由图象可知当直线y＝n与G1、G2的图象共有4个公共点时，n的取值范围为＜n＜2或n＜．
解：（1）根据题意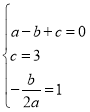得解得，
所以二次函数G1的解析式为y＝﹣x2+2x+3；
（2）因为y＝﹣（x﹣1）2+4，
所以抛物线的顶点坐标为（1，4）；
当x＝﹣1时，y＝0；x＝2时，y＝3；
而抛物线的顶点坐标为（1，4），且开口向下，
所以当﹣1＜x＜2时，0＜y≤4；
（3）G1先向右平移3个单位，再向下平移2个单位，得到新二次函数G2，则函数G2的解析式是y＝﹣（x﹣1﹣3）2+4﹣2，即y＝﹣（x﹣4）2+2，
故答案为y＝﹣（x﹣4）2+2．
（4）解﹣（x﹣4）2+2═﹣（x﹣1）2+4得x＝，
代入y＝﹣（x﹣1）2+4求得y＝，
由图象可知当直线y＝n与G1、G2的图象共有4个公共点时，n的取值范围为＜n＜2或n＜．
