题目内容
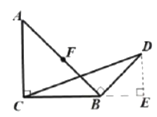
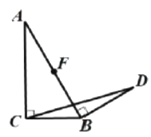
【题目】在![]() 中,
中,![]() 为直径,CD与
为直径,CD与![]() 相较于点H,弧AC=弧AD
相较于点H,弧AC=弧AD
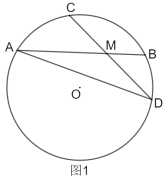
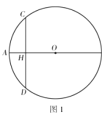
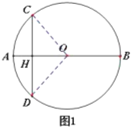
(1)如图1,求证:![]() ;
;
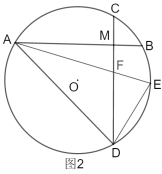
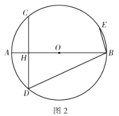
(2)如图2,弧BC上有一点E,若弧CD=弧CE,求证:![]() ;
;
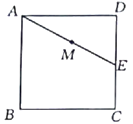
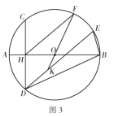
(3)如图3,在(2)的条件下,点F在上,连接![]() ,延长FO交
,延长FO交![]() 于点K,若
于点K,若![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接![]() ,根据
,根据![]() 得出
得出![]() 再根据
再根据![]() 得出
得出![]() ,从而得证;
,从而得证;
(2)连接![]() ,根据
,根据![]() 得出
得出![]() ,
,![]() ,再根据
,再根据![]() ,得出
,得出![]() ,从而得出结论;
,从而得出结论;
(3)作![]() ,过点P作
,过点P作![]() ,
,![]() 先证
先证![]() ,
,![]() ,再证
,再证![]() ,设
,设![]() ,得出
,得出![]() ,再算出
,再算出![]() 得出
得出![]() 为等腰三角形,再根据
为等腰三角形,再根据![]() 是角平分线利用角平分线定理得出
是角平分线利用角平分线定理得出![]() ,从而算出
,从而算出![]() ,再根据三角函数值算出
,再根据三角函数值算出![]() ,
,![]() ,再根据
,再根据![]() 得出
得出![]() ,从而计算
,从而计算![]() .
.
(1)连接OC,CD
因为![]() ,所以
,所以![]()
![]() ,
,![]() ;
;
(2)连接BC,
![]()
所以AB平分![]() ,
,
设![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.

(3) ![]()
设![]()
作![]() ,可证:
,可证:![]() ,
,![]() ,
,
再证:![]()
设![]()
在![]() 中勾股
中勾股![]()
在![]() 中勾股
中勾股![]()
得![]() 为等腰三角形
为等腰三角形
![]()
因为BP为角平分线,过点P作![]()
可证:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目