��Ŀ����
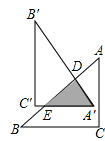
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
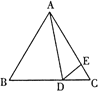
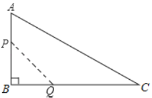
��![]() ������P�ӵ�A��ʼ�ر�AB��B��
������P�ӵ�A��ʼ�ر�AB��B��![]() ���ٶ��ƶ��������B�غϣ�������Q�ӵ�B��ʼ�ر�BC��C��
���ٶ��ƶ��������B�غϣ�������Q�ӵ�B��ʼ�ر�BC��C��![]() ���ٶ��ƶ��������C�غϣ������P��Q�ֱ��A��Bͬʱ���������˶���ʱ��Ϊ
���ٶ��ƶ��������C�غϣ������P��Q�ֱ��A��Bͬʱ���������˶���ʱ��Ϊ![]() ���ı���APQC�����Ϊ
���ı���APQC�����Ϊ![]() ��
��
��1����y��x֮��ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
��2�����ı���APQC���������![]() ʱ����x��ֵ��
ʱ����x��ֵ��
��3���ı���APQC������ܷ����![]() �����ܣ�����˶���ʱ�䣬�����ܣ�˵�����ɣ�
�����ܣ�����˶���ʱ�䣬�����ܣ�˵�����ɣ�
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ��
��![]() ����3�����ܣ����ɼ�����.
����3�����ܣ����ɼ�����.
��������
��1����������ֱ�������ε��������ô𰸼��ɣ�
��2���ں�������ʽ�У���y=112���ⷽ�̼��ɣ�
��3���ں�������ʽ�У���y=172���ⷽ�̼��ɣ�
�⣺��1���߳���ʱ��Ϊx����P���ٶ�Ϊ![]() ����Q���ٶ�Ϊ
����Q���ٶ�Ϊ![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��2��������ã�![]() �����
�����![]() ��
��![]() ��
��
��3�����ܣ����ɣ�
![]() ����ã�
����ã�![]() ��
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
��Ϊ![]() ������
������![]() ���ڷ�Χ�ڣ������ı���APQC��������ܵ���
���ڷ�Χ�ڣ������ı���APQC��������ܵ���![]() ��
��

��ϰ��ϵ�д�
�����Ŀ