题目内容
【题目】已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
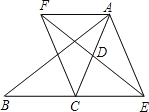
【答案】(1)详见解析;(2)四边形AFCE是矩形,证明详见解析.
【解析】
(1)可通过全等三角形来证明简单的线段相等.△ADF和△CDE中,已知了AD=CD,∠ADF=∠CDE,AF∥BE,因此不难得出两三角形全等,进而可得出AF=CE.
(2)需先证明四边形AFCE是平行四边形,那么对角线相等的平行四边形是矩形.
(1)证明:在△ADF和△CDE中,
∵AF∥BE,
∴∠FAD=∠ECD.
又∵D是AC的中点,
∴AD=CD.
∵∠ADF=∠CDE,
∴△ADF≌△CDE.
∴AF=CE.
(2)解:若AC=EF,则四边形AFCE是矩形.
证明:由(1)知:AF=CE,AF∥CE,
∴四边形AFCE是平行四边形.
又∵AC=EF,
∴平行四边形AFCE是矩形.

练习册系列答案
相关题目