题目内容
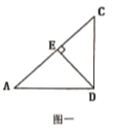
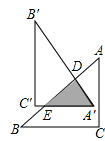
【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8．把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′，A′C′交AB于点E．若AD=BE，则△A′DE的面积是 ．
【答案】6
【解析】
在Rt△ABC中，由勾股定理求得AB=10，由旋转的性质可知AD=A′D，设AD=A′D=BE=x，则DE=10-2x，根据旋转90°可证△A′DE∽△ACB，利用相似比求x，再求△A′DE的面积．
Rt△ABC中，由勾股定理求AB=
=10，
由旋转的性质，设AD=A′D=BE=x，则DE=10﹣2x，
∵△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′，
∴∠A′=∠A，∠A′DE=∠C=90°，
∴△A′DE∽△ACB，
∴=
，即
，解得x=3，
∴S△A′DE=
DE×A′D=×（10﹣2×3）×3=6，故答案为6.
练习册系列答案
名校课堂系列答案
相关题目
