Question

【题目】若关于x的二次函数y＝ax2+bx+c（a，b，c为常数）与x轴交于两个不同的点A（x1，0），B（x2，0）与y轴交于点C，其图象的顶点为点M，O是坐标原点．

（1）若A（﹣2，0），B（4，0），C（0，3）求此二次函数的解析式并写出二次函数的对称轴；

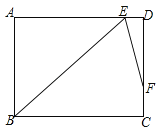
（2）如图，若a＞0，b＞0，△ABC为直角三角形，△ABM是以AB＝2的等边三角形，试确定a，b，c的值；

（3）设m，n为正整数，且m≠2，a＝1，t为任意常数，令b＝3﹣mt，c＝﹣3mt，如果对于一切实数t，AB≥|2t+n|始终成立，求m、n的值．

Answer 1

【答案】（1）y＝﹣x2+x+3 （2），， （3）m＝3，n＝2或m＝6，n＝1

【解析】

（1）先求出a,再代入y＝a（x+2）（x﹣4）＝a（x2﹣2x﹣8）可得；（2）根据等腰三角形性质，先求出点A、B、C的坐标分别为（﹣，0）、（，0），（0，﹣），得函数的表达式为：y＝a（x+）（x﹣）＝a（x2+x﹣），即﹣a＝﹣，求出a可得；（3）由y＝ax2+bx+c＝x2+（3﹣mt）x﹣3mt，得x1+x2＝mt﹣3，x1x2＝﹣3mt，AB＝x2﹣x1＝|mt+3|≥|2t+n|，则m2t2+6mt+9≥4t2+4tn+n2，即：（m2﹣4）t2+（6m﹣4n）t+（9﹣n2）≥0，由题意得：m2﹣4＞0，△＝（6m﹣4n）2﹣4（m2﹣4）（9﹣n2）≤0，解得：mn＝6，再分析出正整数解.

解：（1）函数的表达式为：y＝a（x+2）（x﹣4）＝a（x2﹣2x﹣8），

则﹣8a＝3，解得：a＝﹣，

故抛物线的表达式为：y＝﹣x2+x+3；

（2）如图所示，△ABC为直角三角形，则∠ACB＝90°，

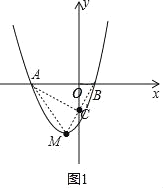
∵△AMB是等边三角形，则点C是MB的中点，

则＝MC＝1，则BO＝BC＝，同理OC＝，

OA＝2﹣＝，

则点A、B、C的坐标分别为（﹣，0）、（，0），（0，﹣），

则函数的表达式为：y＝a（x+）（x﹣）＝a（x2+x﹣），

即﹣a＝﹣，解得：a＝，

则函数表达式为：y＝x2+x﹣；

（3）y＝ax2+bx+c＝x2+（3﹣mt）x﹣3mt，

则x1+x2＝mt﹣3，x1x2＝﹣3mt，

AB＝x2﹣x1＝＝|mt+3|≥|2t+n|，

则m2t2+6mt+9≥4t2+4tn+n2，

即：（m2﹣4）t2+（6m﹣4n）t+（9﹣n2）≥0，

由题意得：m2﹣4＞0，△＝（6m﹣4n）2﹣4（m2﹣4）（9﹣n2）≤0，

解得：mn＝6，

故：m＝3，n＝2或m＝6，n＝1．