题目内容
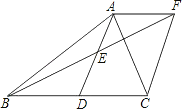
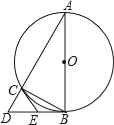
【题目】如图,以△ABC的边AB为直径作⊙O,且顶点C在⊙O上,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=8,BC=6,求BD和CE的长.
【答案】(1)证明见解析;(2)![]() ,
,![]() .
.
【解析】
(1)连接OC,证∠OCE=90°即可;
(2)根据勾股定理可得AB=10,再由tanA=![]() 可得BD的长,然后根据直角三角形斜边上的中线等于斜边一半的性质即得CE的长.
可得BD的长,然后根据直角三角形斜边上的中线等于斜边一半的性质即得CE的长.
(1)证明:连接OC,如图所示:
∵BD是⊙O的切线,
∴∠CBE=∠A,∠ABD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,∠BCD=90°,
∵E是BD中点,
∴CE=![]() BD=BE,
BD=BE,
∴∠BCE=∠CBE=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴∠ACO=∠BCE,
∴∠BCE+∠BCO=90°,
即∠OCE=90°,
∴CE是⊙O的切线;

(2)解:∵∠ACB=90°,
∴AB=![]() ,
,
∵tanA=![]() ,
,
∴BD=![]() AB=
AB=![]() ,
,
∴CE=![]() BD=
BD=![]() .
.

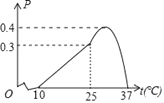
【题目】某农作物的生长率p与温度t(℃)有如下关系:如图,当10≤t≤25时可近似用函数p=![]() t﹣
t﹣![]() 刻画;当25≤t≤37时可近似用函数p=﹣
刻画;当25≤t≤37时可近似用函数p=﹣![]() (t﹣h)2+0.4刻画.
(t﹣h)2+0.4刻画.
(1)求h的值.
(2)按照经验,该作物提前上市的天数m(天)与生长率p之间满足已学过的函数关系,部分数据如下:
生长率p | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m(天) | 0 | 5 | 10 | 15 |
求:①m关于p的函数表达式;
②用含t的代数式表示m.
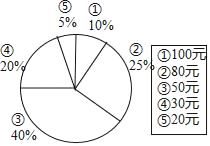
③天气寒冷,大棚加温可改变农作物生长速度.大棚恒温20℃时每天的成本为100元,计划该作物30天后上市,现根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天,但若欲加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天.问加温到多少度时增加的利润最大?并说明理由.(注:农作物上市售出后大棚暂停使用)