Question

【题目】四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG.

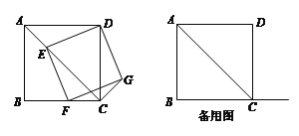
(1)如图，求证：矩形DEFG是正方形；

(2)若AB＝2，CE＝2，求CG的长；

(3)当直线DE与正方形ABCD的某条边所夹锐角是40°时，直接写出∠EFC的度数．

Answer 1

【答案】(1)证明见解析；(2)CG=2； (3)130°或40°.

【解析】

（1）作EP⊥CD于P，EQ⊥BC于Q，证明Rt△EQF≌Rt△EPD，得到EF=ED，根据正方形的判定定理证明即可；

（2）通过计算发现E是AC中点，点F与C重合，△CDG是等腰直角三角形，由此即可解决问题；

（3）分两种情形考虑问题即可．

（1）证明：作EP⊥CD于P，EQ⊥BC于Q，

∵∠DCA=∠BCA，

∴EQ=EP，

∵∠QEF+∠FEC=45°，∠PED+∠FEC=45°，

∴∠QEF=∠PED，

在Rt△EQF和Rt△EPD中，

，

∴Rt△EQF≌Rt△EPD（ASA），

∴EF=ED，

∴矩形DEFG是正方形；

（2）如图2中，在Rt△ABC中．AC=AB=4，

∵EC=2，

∴AE=CE，

∴点F与C重合，此时△DCG是等腰直角三角形，易知CG=2；

（3）①如图3，当DE与AD的夹角为40°时，

∠DEC=45°+40°=85°，

∵∠DEF=90°，

∴∠CEF=5°，

∵∠ECF=45°，

∴∠EFC=130°，

②如图4，当DE与DC的夹角为40°时，

∵∠DEF=∠DCF=90°，

∴∠EFC=∠DEC=40°，

综上所述，∠EFC=130°或40°．