题目内容
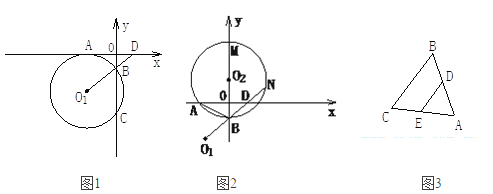
【题目】如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.

(1)求证:四边形ADCE是菱形;
(2)求证:BC=ED.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)由△ABC中,∠ACB=90°,CE是中线,可证得:CE=AE,再由△ACD与△ACE关于直线AC对称,可得:AD=AE=CE=CD,从而可得四边形ADCE是菱形;
(2)由(1)可得DC∥BE,DC=AE=BE,从而可证得:四边形BCDE是平行四边形,就可得到:BC=DE.
试题解析:
(1)证明:∵∠C=90°,点E为AB的中点,
∴EA=EC,
∵△ACD与△ACE关于直线AC对称.
∴△ACD≌△ACE,
∴EA=EC=DA=DC,
∴四边形ADCE是菱形;
(2)∵四边形ADCE是菱形,
∴CD∥AE且CD=AE,
∵AE=EB,
∴CD∥EB且CD=EB
∴四边形BCDE为平行四边形,
∴DE=BC.

练习册系列答案
相关题目