题目内容
【题目】已知二次函数y=ax2+bx+c,当x=3时,y有最小值﹣4,且图象经过点(﹣1,12).
(1)求此二次函数的解析式;
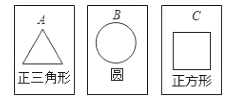
(2)该抛物线交x轴于点A,B(点A在点B的左侧),交y轴于点C,在抛物线对称轴上有一动点P,求PA+PC的最小值,并求当PA+PC取最小值时点P的坐标.
【答案】(1) y=x2﹣6x+5;(2) 当点P的坐标为(3,2)时,PA+PC取最小值,最小值为5![]() .
.
【解析】
(1)由顶点坐标将二次函数的解析式设成y=a(x-3)2-4,由该函数图象上一点的坐标,利用待定系数法即可求出二次函数的解析式;
(2)利用二次函数图象上点的坐标特征可求出点A、B、C的坐标,由二次函数图象的对称性可得出连接BC交抛物线对称轴于点P,此时PA+PC取最小值,最小值为BC,根据点B、C的坐标可求出直线BC的解析式及线段BC的长度,再利用一次函数图象上点的坐标特征即可求出点P的坐标,此题得解.
(1)∵当x=3时,y有最小值-4,
∴设二次函数解析式为y=a(x-3)2-4.
∵二次函数图象经过点(-1,12),
∴12=16a-4,
∴a=1,
∴二次函数的解析式为y=(x-3)2-4=x2-6x+5.
(2)当y=0时,有x2-6x+5=0,
解得:x1=1,x2=5,
∴点A的坐标为(1,0),点B的坐标为(5,0);
当x=0时,y=x2-6x+5=5,
∴点C的坐标为(0,5).
连接BC交抛物线对称轴于点P,此时PA+PC取最小值,最小值为BC,如图所示.
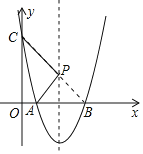
设直线BC的解析式为y=mx+n(m≠0),
将B(5,0)、C(0,5)代入y=mx+n,得:
![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为y=-x+5.
∵B(5,0)、C(0,5),
∴BC=5![]() .
.
∵当x=3时,y=-x+5=2,
∴当点P的坐标为(3,2)时,PA+PC取最小值,最小值为5![]() .
.