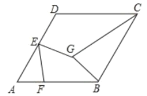
题目内容
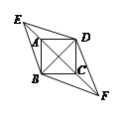
【题目】如图,BD是ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
【答案】![]() .
.
【解析】
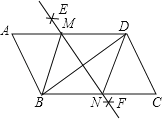
由作法得MN垂直平分BD,则MB=MD,NB=ND,再证明△BMN为等腰三角形得到BM=BN,则可判断四边形BMDN为菱形,利用菱形的性质和勾股定理计算出BN=5,然后利用面积法计算![]() 的边BC上的高.
的边BC上的高.
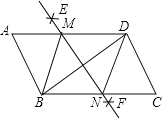
由作法得MN垂直平分BD,
∴MB=MD,NB=ND,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠MDB=∠NBD,
而MB=MD,
∴∠MBD=∠MDB,
∴∠MBD=∠NBD,
而BD⊥MN,
∴△BMN为等腰三角形,
∴BM=BN,
∴BM=BN=ND=MD,
∴四边形BMDN为菱形,
∴![]() ,
,
设ABCD的边BC上的高为h,
∵![]() ,
,
∴![]() ,
,
即ABCD的边BC上的高为![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目