题目内容
【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.
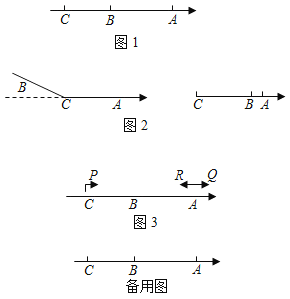
(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
【答案】(1)点C到原点的距离为20;(2)C点在数轴上对应的数是﹣4或﹣3;(3)动点Q的速度为1个单位长度/秒
【解析】
(1)由题意列出方程可求解;
(2)分两种情况讨论,列出方程可求解;
(3)设点R的速度为y,则点P的速度3y,点Q的速度是2y﹣5,由点P、Q之间的距离是点Q、R之间距离的一半,列出方程求解即可.
(1)设点C表示的数为a.
∵BC:AB=3:5,
∴(﹣11﹣a):(4+11)=3:5,
∴a=﹣20,
∴点C到原点的距离为20;
(2)设点C表示的数为x,
根据题意得:(4﹣x)﹣(x+11)=1,或(x+11)﹣(4﹣x)=1,
∴x=﹣4或﹣3,
∴C点在数轴上对应的数是﹣4或﹣3;
(3)设点R的速度为y个单位长度/秒,则点P的速度3y个单位长度/秒,点Q的速度是(2y﹣5)个单位长度/秒,
由题意得:|(﹣20+4×3y)﹣[4+4(2y﹣5)]|![]() 4×(y+2y﹣5)
4×(y+2y﹣5)
解得:y=3或1.4,
∴2y﹣5=1或﹣2.2(不合题意舍去).
答:动点Q的速度为1个单位长度/秒.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目