题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() 的最大值为_____.
的最大值为_____.
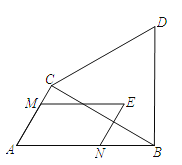
【答案】![]()
【解析】
作辅助线,构建30度的直角三角形将![]() 转化为NH,将,即:过A点作AM∥BC,过
转化为NH,将,即:过A点作AM∥BC,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,由△BCD围成的区域(包括各边)内的一点到直线AP的最大值时E在D点时,通过直角三角形性质和勾股定理求出DH’即可得到结论.
,由△BCD围成的区域(包括各边)内的一点到直线AP的最大值时E在D点时,通过直角三角形性质和勾股定理求出DH’即可得到结论.
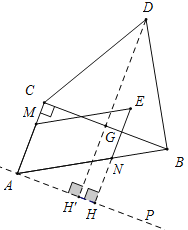
解:过A点作AP∥BC,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
设![]() ,
,![]() ,
,
∵∠ACB=90°,∠CAB=60°,
∴∠CAM=90°,∠NAH=30°,
![]() 中,
中,![]() ,
,
∵NE∥AC,NH∥AC,
∴E、N、H在同一直线上,
![]()
![]() ,
,
由图可知:△BCD围成的区域(包括各边)内的一点到直线AM距离最大的点在D点,
过D点作![]() ,垂足为
,垂足为![]() .
.
当![]() 在点
在点![]() 时,
时,![]() =
=![]() 取最大值.
取最大值.
∵∠ACB=90°,∠A=60°,AB=6,,
∴AC=3,AB=![]() ,四边形ACGH’是矩形,
,四边形ACGH’是矩形,
∴![]() ,
,
∵△BCD为等边三角形,![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() 的最大值为
的最大值为![]() ,
,
故答案为:![]() .
.

【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 |
|
|
|
|
| ······ |
油箱中的剩余油量 |
|
|
|
|
| ····· |
(1)在这个问题中,自变量是_ 因变量是_ ;
(2)该轿车油箱的容量为__ L,行驶![]() 时,估计油箱中的剩余油量为____
时,估计油箱中的剩余油量为____![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请估计
,请估计![]() 两地之间的距离.
两地之间的距离.