题目内容
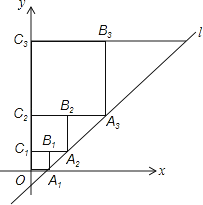
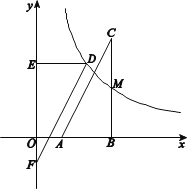
【题目】如图,在平面直角坐标系xOy中,Rt△ABC的直角边AB在x轴上,∠ABC=90°.点A的坐标为(1,0),点C的坐标为(3,4),M是BC边的中点,函数![]() (
(![]() )的图象经过点M.
)的图象经过点M.
(1)求k的值;
(2)将△ABC绕某个点旋转180°后得到△DEF(点A,B,C的对应点分别为点D,E,F),且EF在y轴上,点D在函数![]() (
(![]() )的图象上,求直线DF的表达式.
)的图象上,求直线DF的表达式.
【答案】(1)6;(2)y=2x-1.
【解析】
(1)根据直角三角形的性质和坐标与图形的特点求得点![]() 的坐标,将其代入反比例函数解析式求得
的坐标,将其代入反比例函数解析式求得![]() 的值;
的值;
(2)根据旋转的性质推知:![]() ,故其对应边、角相等:
,故其对应边、角相等:![]() ,
,![]() ,
,![]() ,由函数图象上点的坐标特征得到:
,由函数图象上点的坐标特征得到:![]() ,
,![]() .结合
.结合![]() 得到
得到![]() ,利用待定系数法求得结果.
,利用待定系数法求得结果.
(1)∵Rt△ABC的直角边AB在x轴上,∠ABC=90°,点C的坐标为(3,4),
∴点B的坐标为(3,0),CB=4.
∵M是BC边的中点,
∴点M的坐标为(3,2).
![]()
∴k=3×2=6.
(2)∵△ABC绕某个点旋转180°后得到△DEF,
∴△DEF≌△ABC.
∴DE=AB,EF=BC,∠DEF=∠ABC=90°.
∵点A的坐标为(1,0),点B的坐标为(3,0),
∴AB=2.
∴DE=2.
∵EF在y轴上,
∴点D的横坐标为2.
![]()
当x=2时,y=3.
∴点D的坐标为(2,3).
∴点E的坐标为(0,3).
∵EF=BC=4,
∴点F的坐标为(0,-1).
设直线DF的表达式为y=ax+b,将点D,F的坐标代入,
![]()
∴直线DF的表达式为y=2x-1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小梅在浏览某电影评价网站时,搜索了最近关注到的甲、乙、丙三部电影,网站通过对观众的抽样调查,得到这三部电影的评分数据统计图分别如下:
甲、乙、丙三部电影评分情况统计图
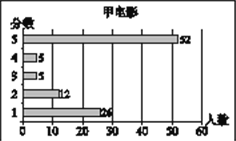


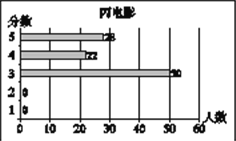
根据以上材料回答下列问题:
(1)小梅根据所学的统计知识,对以上统计图中的数据进行了分析,并通过计算得到这三部电影抽样调查的样本容量,观众评分的平均数、众数、中位数,请你将下表补充完整:
甲、乙、丙三部电影评分情况统计表
电影 | 样本容量 | 平均数 | 众数 | 中位数 |
甲 | 100 | 3.45 | 5 | |
乙 | 3.66 | 5 | ||
丙 | 100 | 3 | 3.5 |
(2)根据统计图和统计表中的数据,可以推断其中_______电影相对比较受欢迎,理由是
_______________________________________________________________________.(至少从两个不同的角度说明你推断的合理性)
【题目】为了庆祝即将到来的2018年国庆节,某校举行了书法比赛,赛后整理了参赛同学的成绩,并制作了如下两幅不完整的统计图表
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= .
(2)请补全频数直方图;
(3)若绘制扇形统计图,则分数段60≤x<70所对应的扇形的圆心角的度数是 .