题目内容
【题目】问题发现:
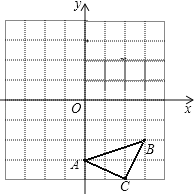
(![]() )如图①,点
)如图①,点![]() 和点
和点![]() 均在⊙
均在⊙![]() 上,且
上,且![]() ,点
,点![]() 和点
和点![]() 均在射线
均在射线![]() 上,若
上,若![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置关系是__________;若
的位置关系是__________;若![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置关系是__________.
的位置关系是__________.
问题解决:
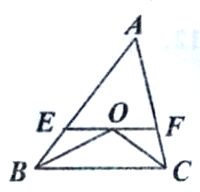
如图②,图③所示,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是
是![]() 边上任意一点.
边上任意一点.
(![]() )当
)当![]() 时,求
时,求![]() 的长度.
的长度.
(![]() )是否存在点
)是否存在点![]() ,使得
,使得![]() 最大?若存在,请说明理由,并求出
最大?若存在,请说明理由,并求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



【答案】(![]() )点
)点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 外;(
外;(![]() )
)![]() 或
或![]() ;(
;(![]() )当
)当![]() 有最大值时,
有最大值时, ![]() 长为
长为![]() .
.
【解析】试题分析:(1)根据题意得:点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 外;
外;
(2)以AD为斜边等腰直角三角形AOD ,以点O为圆心,OA为半径作⊙O交BC于点E.在RtΔAOD中可计算OA=2,连接OP,则OP=PA=2,过点![]() 作
作![]() 于点
于点![]() ,可求出BO=2,再进而求出BC的值,确定点P的个数;
,可求出BO=2,再进而求出BC的值,确定点P的个数;
(3)存在.
试题解析:(1)点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 外;
外;
(![]() )以
)以![]() 为斜边等腰直角三角形
为斜边等腰直角三角形![]() ,
,
以点![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() 交
交![]() 于点
于点![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴ ![]() ,
,
连接![]() ,则
,则![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
, ![]() ,∴
,∴ ![]() .
.
又∵![]() ,∴四边形
,∴四边形![]() 为矩形,
为矩形,
∴![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() .
.
又∵经计算![]() ,
,
∴符合条件的点![]() 有
有![]() 个.
个.
![]() 的长为
的长为![]() 或
或![]() .
.
(![]() )存在,作
)存在,作![]() 的中垂线,交
的中垂线,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在
,在![]() 上取点
上取点![]() ,
,
以![]() 为半径作⊙
为半径作⊙![]() ,当⊙
,当⊙![]() 与
与![]() 相切于点
相切于点![]() 时,
时, ![]() 最大.
最大.
理由:在![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
, ![]() 交⊙
交⊙![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
∵![]() ,
, ![]() ,∴
,∴ ![]() ,
,
∴![]() 和
和![]() 均为等腰直角三角形.
均为等腰直角三角形.
∴![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,
, ![]() ,
,
∵⊙![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,∴
,∴ ![]() ,
,
又∵![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴设![]() ,则
,则![]() ,
, ![]()
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
解得: ![]() (舍),
(舍),![]() ,
,
∴![]() ,
,
∴当![]() 有最大值时,
有最大值时, ![]() 长为
长为![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目