题目内容
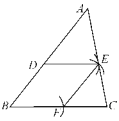
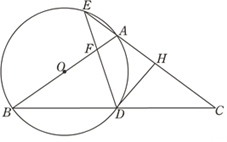
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】分析:(1)由角的关系易证OD//AC,已知![]() 即证
即证![]()
(2)由OD//AC,可证![]() 根据“相似三角形的对应边成比例”易得
根据“相似三角形的对应边成比例”易得![]() , 设
, 设![]() 证明
证明![]()
![]() 是等腰三角形,表示出
是等腰三角形,表示出![]() 即可证明.
即可证明.
(3)通过等量关系表示出边的长度,由![]() 可得对应边的比例关系的方程,求解即可.
可得对应边的比例关系的方程,求解即可.
详解:(1)连接OD,如图1,
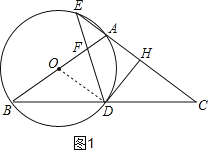
∵在⊙O中,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴OD//AC,
∵![]()
∴![]()
∴![]()
∴![]()
∴DH是圆O的切线;
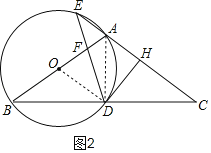
(2)∵![]()
∴![]()
∴![]() ,
,
设![]()
连接AD,
∵AB是直径,
∴∠ADB=90°,即![]()
∵![]()
∴D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC, ![]()
∴![]()
∵在⊙O中,![]()
∴![]()
∴![]() 是等腰三角形,
是等腰三角形,
∵![]()
∴![]()
∵A在EH上且![]() ,
,
∴A为EH的中点.
(3)如图2,设⊙O的半径为r,即![]()
∵![]()
∴![]()
∵OD∥EC,
∴![]()
则![]()
∴![]()
∴![]()
∴![]()
在⊙O中,∵![]()
∴![]()
∴![]() ,
,![]() 是等腰三角形,
是等腰三角形,
∴![]()
∴![]()
∵![]()
∴![]()
![]()
![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),
综上所述,⊙O的半径为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目