题目内容
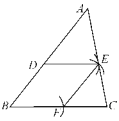
【题目】如图,在△ABC中,D是AB上的一点,进行如下操作:①以B为圆心,BD长为半径作弧交BC于点F;②再分别以D,F为圆心,BD长为半径作弧,两弧恰好相较于AC上的点E处;③连接DE,FE.若AB=6,BC=4,那么AD=________.
【答案】3.6
【解析】分析:根据作图可知四边形BFED是菱形,然后根据△ADE∽△ABC即可求出.
详解: :∵根据作法可知:
BD=BF=EF=DE,
∴四边形AEDF是菱形,
∵DE∥AC,
∴![]()
设AD=x,则DE=6-x,
∵AB=6,BC=4,
∴ ![]() ,
,
∴AD=3.6.
点睛: 本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.

 名校课堂系列答案
名校课堂系列答案【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
【题目】随着教育教学改革的不断深入,应试教育向素质教育转轨的力度不断加大,体育中考已成为初中毕业升学考试的重要内容之一。为了解某市九年级学生中考体育成绩情况,现从中随机抽取部分考生的体育成绩进行调查,并将调查结果绘制如下图表:
2019年中考体育成绩(分数段)统计表 | ||
分数段 | 频数(人) | 频率 |
25≤x<30 | 12 | 0.05 |
30≤x<35 | 24 | b |
35≤x<40 | 60 | 0.25 |
40≤x<45 | a | 0.45 |
45≤x<50 | 36 | 0.15 |
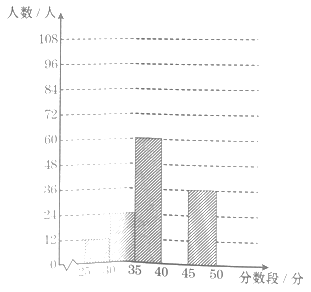
根据上面提供的信息,回答下列问题:
(1)表中a和b所表示的数分别为a=______,b=______;并补全频数分布直方图;
(2)甲同学说“我的体育成绩是此次抽样调查所得数据的中位数。”请问:甲同学的体育成绩在______分数段内?
(3)如果把成绩在40分以上(含40分)定为优秀那么该市12000名九年级考生中考体育成绩为优秀的约有多少名?