题目内容
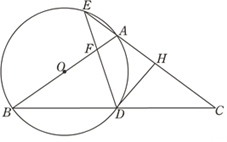
【题目】如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,点D关于AB,AC的对称点分别是点E,F,四边形AEGF是平行四边形,则四边形AEGF面积的最小值是 ( )

A. 1B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由对称的性质和菱形的定义证出四边形AEGF是菱形,得出∠EAF=2∠BAC=120°,当AD⊥BC最小时,AD的值最小,即AE的值最小,即菱形AEGF面积最小,求出AD=![]() ,即可得出四边形AEGF的面积的最小值.
,即可得出四边形AEGF的面积的最小值.
由对称的性质得:AE=AD=AF,
∵四边形AEGF是平行四边形,
∴四边形AEGF是菱形,
∴∠EAF=2∠BAC=120°,
当AD⊥BC最小时,AD的值最小,即AE的值最小,即菱形AEGF面积最小,
∵∠ABC=45°,AB=2,
∴AD=![]() ,
,
∴四边形AEGF的面积的最小值=![]() .
.
故选:D

练习册系列答案
相关题目