Question

【题目】如图，在平行四边形ABCD中，点E、F分别在BC、AD上，且∠BAE=∠DCF．

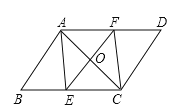
（1）求证：△ABE≌△CDF；

（2）若AC⊥EF，试判断四边形AECF是什么特殊四边形，并证明你的结论．

Answer 1

【答案】（1）证明见解析；（2）四边形AECF是菱形，证明见解析．

【解析】

试题分析：（1）由平行四边形ABCD可得∠B=∠D，AB=CD，根据已知给出的∠BAE=∠DCF，可证明两个三角形全等．

（2）可先确定四边形AECF中对角线的关系，再根据AC⊥EF，从而判断出到底是什么特殊的四边形．

试题解析：（1）∵在平行四边形ABCD中，∴∠B=∠D，AB=CD，又∵∠BAE=∠DCF．∴△ABE≌△CDF；

（2）四边形AECF是菱形．证明如下：

∵△ABE≌△CDF，∴BE=DF，∴BC﹣BE=AD﹣FD，∴EC=AF，∵AD∥BC，∴∠FAC=∠ECA，∠CEF=∠AFE，∴△AOF≌△COE，∴AO=CO，EO=FO，又∵AC⊥EF，∴四边形AECF是菱形．