Question

【题目】如图，已知∠AOB内部有三条射线，OE平分∠BOC，OF平分∠AOC．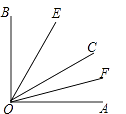

（1）若∠AOB=90°，∠AOC=40°，求∠EOF的度数；
（2）若∠AOB=a，求∠EOF的度数．

Answer 1

【答案】
（1）解：∠BOC=∠AOB﹣∠AOC=90°﹣40°=50°，

∵OE平分∠BOC，OF平分∠AOC，

∴∠EOC= ∠BOC= ×50°=25°，∠COF= ∠AOC= ×40°=20°，

∴∠EOF=∠EOC+∠COF=25°+20°=45°

（2）解：∵OE平分∠BOC，OF平分∠AOC，

∴∠EOC= ∠BOC，∠COF= ∠AOC，

∴∠EOF=∠EOC+∠COF= ∠BOC+ ∠COF= （∠BOC+∠AOC）= ∠AOB= α

【解析】（1）首先求得∠BOC，然后根据角的平分线的定义求得∠EOC和∠COF，然后根据∠EOF=∠EOC+∠COF求解；（2）根据角的平分线的定义求得∠EOC= ∠BOC，∠COF= ∠AOC，然后根据∠EOF=∠EOC+∠COF= ∠BOC+ ∠COF= （∠BOC+∠AOC）即可求解．
【考点精析】关于本题考查的角的平分线，需要了解从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线才能得出正确答案．