题目内容
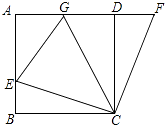
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论: ①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .
.
其中正确的序号是(把你认为正确的都填上).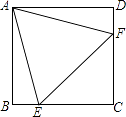
【答案】①②④
【解析】解:∵四边形ABCD是正方形, ∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF= ![]() ,
,
设正方形的边长为a,
在Rt△ADF中,
AD2+DF2=AF2 , 即a2+(a﹣ ![]() )2=4,
)2=4,
解得a= ![]() ,
,
则a2=2+ ![]() ,
,
S正方形ABCD=2+ ![]() ,
,
④说法正确,
所以答案是:①②④.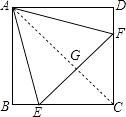
【考点精析】关于本题考查的等边三角形的性质和正方形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目