题目内容
【题目】如图，在△ABC中，∠C=90°，∠CAB=30°，AB=10，点D在线段AB上，AD=2．点P，Q以相同的速度从D点同时出发，点P沿DB方向运动，点Q沿DA方向到点A后立刻以原速返回向点B运动．以PQ为直径构造⊙O，过点P作⊙O的切线交折线AC﹣CB于点E，将线段EP绕点E顺时针旋转60°得到EF，过F作FG⊥EP于G，当P运动到点B时，Q也停止运动，设DP=m． 
（1）当2＜m≤8时，AP=，AQ=．（用m的代数式表示）
（2）当线段FG长度达到最大时，求m的值；
（3）在点P，Q整个运动过程中， ①当m为何值时，⊙O与△ABC的一边相切？
②直接写出点F所经过的路径长是．（结果保留根号）
【答案】
（1）解：当2＜m≤8时，AP=2+m，AQ=m﹣2．
故答案为2+m，m﹣2．
（2）解：如图1中，
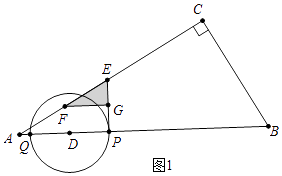
在Rt△EFG中，∵∠EFG=∠A=30°，∠EGF=90°，
∴FG=EFcos30°=PEcos30°= 
EP，
∴当点E与点C重合时，PE的值最大，
易知此时EP= 
= 
= 
，
∵EP=APtan30°=（2+m） 
，
∴ =（2+m） ，
∴m=5.5
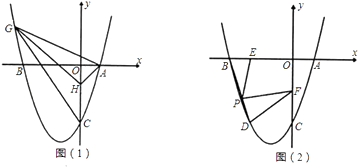
（3）解：①当0＜t≤2（Q在往A运动）时，如图2中，设⊙O切AC于H，连接OH．
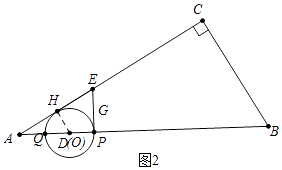
则有AD=2DH=2，
∴DH=DQ=1，即m=1．
当2＜t≤8（Q从A向B运动）时，则PQ=（2+m）﹣（m﹣2）=4，
如图3中，设⊙O切AC于H．连接OH．
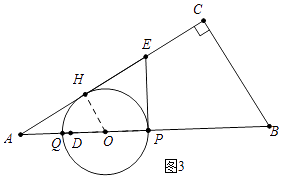
则AO=2OH=4，AP=4+2=6，
∴2+m=6，
∴m=4．
如图4中，设⊙O切BC于N，连接ON．
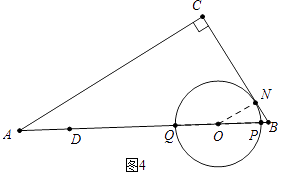
在Rt△OBN中，OB= 
= 
，
∴AO=10﹣ ，
∴AP=12﹣ 
，
∴2+m=12﹣ ，
∴m=10﹣ ，
综上所述，当m=1或4或10﹣ 时，⊙O与△ABC的边相切．
②如图5中，点F的运动轨迹是F1→F2→B．
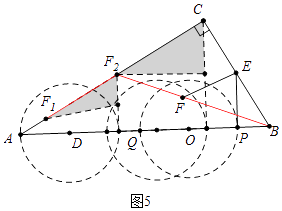
易知AF1= 
，CF2= ，AC=5 
，
∴F1F2=5 ﹣ 
﹣ = 
，
∵∠FEP=60°，∠PEB=30°，
∴∠FEB=90°，
∴tan∠EBF= 
= 
为定值，
∴点F的第二段的轨迹是线段BF2，
在Rt△BF2C中，BF2= 
= 
= 
，
∴点F的运动路径的长为 
+ ．
【解析】（1）根据题意可得AP=2+m，AQ=m﹣2．（2）如图1中，在Rt△EFG中，∠EFG=∠A=30°，∠EGF=90°，推出FG=EFcos30°=PEcos30°= EP，所以当点E与点C重合时，PE的值最大，求出此时EP的长即可解决问题．（3）①分三种情形讨论：当0＜t≤2（Q在往A运动）时，如图2中，设⊙O切AC于H，连接OH．当2＜t≤8（Q从A向B运动）时，则PQ=（2+m）﹣（m﹣2）=4，如图3中，设⊙O切AC于H．连接OH．如图4中，设⊙O切BC于N，连接ON．分别求解即可．②如图5中，点F的运动轨迹是F1→F2→B．分别求出F1F2 ， F2B即可解决问题．
