Question

【题目】如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:

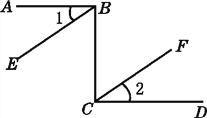
因为AB⊥BC,DC⊥BC,

所以∠ABC=90°,

∠BCD=90°(______________),

所以∠ABC=∠BCD.

又因为∠1=∠2,

所以∠EBC=∠FCB.

所以BE∥CF(______________).

Answer 1

【答案】垂直的定义;内错角相等,两直线平行

【解析】试题分析：题中已知AB⊥BC，DC⊥BC，根据垂直的定义可得∠ABC=∠BCD=90°，又因为∠1=∠2，由等量减等量，差相等可得∠EBC=∠FCB，观察图形可知，∠EBC与∠FCB是直线BE与CF被直线BC所截的内错角，即可得证.

试题解析：因为AB⊥BC，DC⊥BC（已知），

所以∠ABC=∠BCD=90°（垂直的定义）.

又因为∠ABC-∠1=∠BCD-∠2，

即∠EBC=∠FCB，

所以BE∥CF（内错角相等，两直线平行）.

故答案为：垂直的定义；内错角相等，两直线平行.