题目内容
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值.
【答案】
(1)
解:∵四边形ABCD是正方形,
∴∠BCF=∠DCE=90°
∵AC是正方形ABCD的对角线,
∴∠ACB=∠ACD=45°,
∴∠ACF=∠ACE,
∵∠EAF被对角线AC平分,
∴∠CAF=∠CAE,
在△ACF和△ACE中, 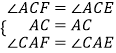 ,
,
∴△ACF≌△ACE,
∴CF=CE,
∵CE=a,CF=b,
∴a=b,
∵△ACF≌△ACE,
∴∠AEF=∠AFE,
∵∠EAF=45°,
∴∠AEF=∠AFE=67.5°,
∵CE=CF,∠ECF=90°,∠AEC=∠AFC=22.5°,
∵∠CAF=∠CAE=22.5°,
∴∠CAE=∠CEA,
∴CE=AC=4 ![]() ,即:a=b=4
,即:a=b=4 ![]()
(2)
解:当△AEF是直角三角形时,
①如图所示:

∵∠AFE=90°,
∴∠AFD+∠CFE=90°,
∵∠CEF+∠CFE=90°,
∴∠AFD=∠CEF
∵∠AFE=90°,∠EAF=45°,
∴∠AEF=45°=∠EAF∴AF=EF,
在△ADF和△FCE中 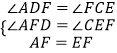 ,
,
∴△ADF≌△FCE,
∴FC=AD=4,CE=DF=CD+FC=8,
∴a=8,b=4.
②当∠AEF=90°时,同①的方法得,CF=4,CE=8,
∴a=4,b=8
【解析】(1)先证明△ACF≌△ACE,从而得到CF=CE,然后再证明△ACE为等腰三角形,则CE=AC=4 ![]() ;(2)当∠AFE=90°,可证明△ADF≌△FCE,则FC=AD=4,CE=DF=CD+FC=8,从而可求得a、b的值,同理当∠AEF=90°时,也可求得a、b的值.
;(2)当∠AFE=90°,可证明△ADF≌△FCE,则FC=AD=4,CE=DF=CD+FC=8,从而可求得a、b的值,同理当∠AEF=90°时,也可求得a、b的值.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案