题目内容
【题目】如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( ) 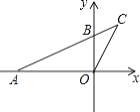
A.(1, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2
,2 ![]() )
)
D.( ![]() ,2
,2 ![]() )
)
【答案】B
【解析】解:∵A(﹣4,0),B(0,2), ∴OA=4,OB=2,
∵△COB∽△CAO,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴CO=2CB,AC=2CO,
∴AC=4CB,
∴ ![]() =
= ![]() ,
,
过点C作CD⊥y轴于点D,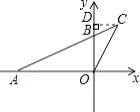
∵AO⊥y轴,
∴AO∥CD,
∴△AOB∽△CDB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴CD= ![]() AO=
AO= ![]() ,
,
BD= ![]() OB=
OB= ![]() ,
,
∴OD=OB+BD=2+ ![]() =
= ![]() ,
,
∴点C的坐标为( ![]() ,
, ![]() ).
).
故选B.
根据相似三角形对应边成比例求出CB、AC的关系,从而得到 ![]() =
= ![]() ,过点C作CD⊥y轴于点D,然后求出△AOB和△CDB相似,根据相似三角形对应边成比例求出CD、BD,再求出OD,最后写出点C的坐标即可.
,过点C作CD⊥y轴于点D,然后求出△AOB和△CDB相似,根据相似三角形对应边成比例求出CD、BD,再求出OD,最后写出点C的坐标即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目