题目内容
【题目】如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°. 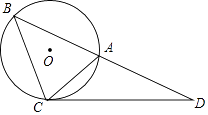
(1)求证:CD是⊙O的切线;
(2)求 ![]() 的长.
的长.
【答案】
(1)证明:连接OA、OC.则∠AOC=2∠ABC=90°,
∵在△AOC中,OA=OC,
∴∠OCA=∠OAC=45°,
又∵∠ACD=45°,
∴∠OCD=∠OCA+∠ACD=45°+45°=90°,
∴OC⊥CD.
即CD是⊙O的切线
(2)解:连接OB.
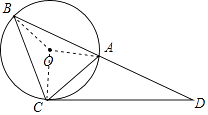
∵∠ABC=45°,∠D=30°,∠ACD=∠ABC=45°,
∴在△BCD中,∠BCD=180°﹣∠ABC﹣∠D=180°﹣45°﹣30°=105°,
∴∠ACB=∠BCD﹣∠ACD=105°﹣45°=60°,
∴∠AOB=2∠ACB=120°,
∴ ![]() 的长为:
的长为: ![]() =
= ![]() .
.
【解析】(1)证明:连接OA、OC,得到∠AOC=2∠ABC=90°,求得∠OCA=∠OAC=45°,于是得到OC⊥CD.由切线的判定定理即可得到结论;(2)连接OB.根据三角形的内角和得到∠ACB=∠BCD﹣∠ACD=105°﹣45°=60°,由圆周角定理得到∠AOB=2∠ACB=120°,根据弧长公式即可得到结论.
【考点精析】通过灵活运用三角形的外接圆与外心和切线的判定定理,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.

【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别 | 成绩x(分) | 频数(人数) |
A | 8.0≤x<8.5 | a |
B | 8.5≤x<9.0 | 8 |
C | 9.0≤x<9.5 | 15 |
D | 9.5≤x<10 | 3 |

(1)图中a= , 这次比赛成绩的众数落在组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.