题目内容
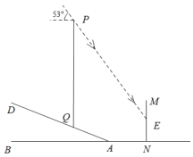
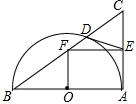
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
【答案】(1) ![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或20.
或20.
【解析】
(1)设BD与AM交于点N,那么∠BNM=90°,BN=DN,然后解直角三角形即可解答;
(2)先确定∠CAB的正弦值,再设BG=3m、OG=4m建立方程求得m;再运用解直角三角形求得BE,最后利用AE=AB-BE即可求解;
(3)先求出△AOE为等腰三角形时圆O的半径及圆心距;然后就圆A与圆O是内切还是外切分类讨论求解即可.
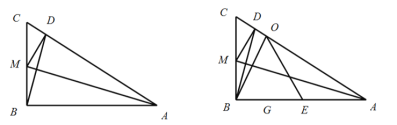
解:(1)如图:设BD与AM交于点N,那么∠BNM=90°,BN=DN
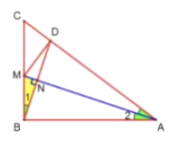
∵Rt△ABM中,AB=12,BM=4,
∴tan∠2=![]() , cos∠2=
, cos∠2=![]()
∵∠1+∠BMN=90°,∠2+∠BMN=90°,
∴∠1=∠2.
∵Rt△BMN中,BM=4,
∴BN=BM·cos∠1=![]()
∴BD=2BN=![]()
如图所示:作DH⊥AB于H,
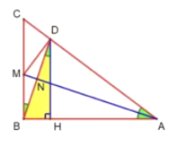
∴DH∥CB
∴∠BDH=∠MBN
∴DH=BD·cos∠BDH=![]() ×
×![]() =
=![]() ;
;
(2)∵在Rt△ADH中,DH=![]() ,AD=AB=12,
,AD=AB=12,
∴sin∠CAB=![]()
如图所示:因为点F平分弧BE,
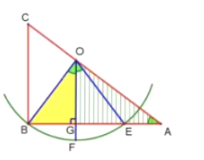
∴OF⊥BE,BG=EG
在Rt△BOG中,已知∠BOF=∠BAC,设BG=3m,OG=4m.
在Rt△AOG中,由tan∠A=![]() =
=![]() ,
,
解得m=![]()
∴AE=AB-BE=12-6m=![]() ;
;
(3)第一步,求△AOE为等腰三角形时圆O的半径,
∵△AOE是钝角三角形,
∴只存在EO=EA的情况。
如图所示:作EK⊥AC于K
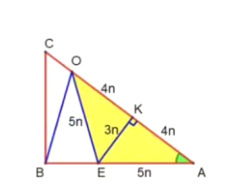
在Rt△AEK中,设EK=3n,则AK=4n,EA=5n.
如图所示:作OP⊥AB于P
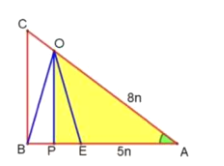
在Rt△AOP中,OA=2AK=8n,AP=![]() OA=
OA=![]()
∴PE=AP-AE=![]() -5n=
-5n=![]()
由AB=2PE+EA=![]() +5n=12.解得:n=
+5n=12.解得:n=![]() .
.
∴ro=OE=5n=![]() ,圆心距d=OA=
,圆心距d=OA=![]()
第二步,分两种情况讨论圆A与圆O相切.
①如图所示,当圆A与圆O外切时,ro+ra=d,
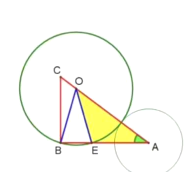
所以ra =d-ro=![]() ;
;
②如图所示,当圆A与圆O内切时ra-ro=d
所以ra=d+ro=![]() .
.