Question

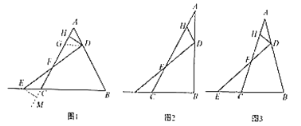
【题目】重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号，保证广大师生网络授课、听课的质量，临时在坡度为的山坡上加装了信号塔（如图所示），信号塔底端到坡底的距离为3.9米．同时为了提醒市民，在距离斜坡底4.4米的水平地面上立了一块警示牌．当太阳光线与水平线成53°角时，测得信号塔落在警示牌上的影子长为3米，则信号塔的高约为（tan53°≈1.3）（ ）.

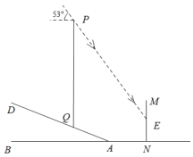
A.10.4B.11.9C.11.4D.13.4

Answer 1

【答案】B

【解析】

过点E作EH⊥PQ于点H，延长PQ交AB于点G，利用已知条件可得到AQ，AN，EN的长及∠PEH的度数，同时可得四边形HGNE是矩形，就可推出EN=HG=3米，HE=GN，利用坡度的定义及勾股定理求出QG，AG的长，由此可得到HE，QH的长，然后利用解直角三角形求出PH的长，根据PQ=PH+QH，就可求出PQ的长.

解：过点E作EH⊥PQ于点H，延长PQ交AB于点G，

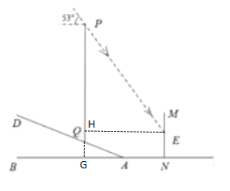
由题意可知：∠PEH=53°，AQ=3.9米，AN=4.4米，EN=3米，四边形HGNE是矩形，

∴EN=HG=3米，HE=GN，

∵AD的坡度为i=1：2.4，

∴QG：AG=1：2.4，

设QG=x，则AG=2.4x，

在Rt△AQG中，AG2+QG2=AQ2，即x2+（2.4x）2=3.92，

解得：x=1.5，

∴AG=1.5×2.4=3.6，QG=1.5，

∴HE=NG=AG+AN=3.6+4.4=8，HQ=HG-QG=3-1.5=1.5，

在Rt△PHE中，PH=HE·tan∠PEH=8tan53°≈8×1.3=10.4米，

∴PQ=PH+QH=10.4+1.5=11.9米，

故答案为：B.