Question

【题目】如图，在平面直角坐标系中，抛物线y=ax-4ax交x轴于点A，直线y= x+3与x轴交于点B，与y轴交于点C，与抛物线交于点D，E(点D在点E的右侧)．

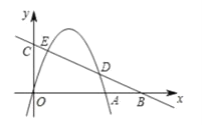
（1）求点A，B，C的坐标．

（2）当点D为BC的中点时，求a的值．

（3）若设抛物线的顶点为点M，点M关于直线BC的对称点为N， 当点N落在△BOC的内部时，求a的取值范围．

Answer 1

【答案】（1）A(4，0)，B(6，0)，C(0，3)；（2）a=；（3）<a<

【解析】

（1）利用抛物线的解析式求出点A的坐标，再利用一次函数解析式，由y=0求出对应的x的值，由x=0求出对应的y的值，即可得到点B，C的坐标；

（2）利用中点坐标求出点D的坐标，再将点D的坐标代入抛物线的解析式求出a的值；（3）将函数解析式转化为顶点式，可得到顶点M的坐标，再分情况讨论：当N恰好落存OC上时，作MH⊥y轴，连接CM，易证△HMN∽△OCB，利用已知求出a的值；当N落在x轴上时，可以求得Ｎ不在OB内(N不可能在线段OB上)；当N落在BC上时，则M也在BC上，易求出a的值，即可得到a的取值范围.

（1）解：∵抛物线y=ax2-4ax交x轴于点A，

∴当y=0时， ，

解得，

∴A(4，0)，

∵直线y=x+3与x轴交于点B，与y轴交于点C，

∴当y=0时得x=6，当x=0时得y=3，

∴B(6，0)，C(0，3)．

（2）解：∵点D为BC的中点，

∴点D的坐标为(3， )，

把(3， )代入y=ax2-4ax得a=，

（3）解：由y=ax2-4ax=a(x-2)2-4a，∴M(2，-4a) ，

当N恰好落在OC上时，作MH⊥y轴，连接CM，

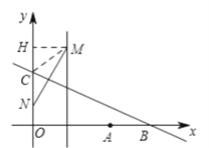
∴MN⊥BC，

∴∠MNH+∠OCB=90°，

∵∠OCB+∠OBC=90°，

∴∠MNH=∠OBC，

∵∠MHN=∠COB=90°，

∴△HMN∽△OCB，

∴ ，

∵HM=2，OC=3，OB=6，

∴HN=4，

∵CM=CN，

∴在Rt△HCM中利用勾股定理，得CN=CM= ，CH=，

∴OH=，

∴-4a=，

∴a=；

当N落在x轴上时，可以求得N不在OB内(N不可能在线段OB上)；

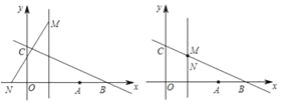
当N落在BC上时，则M也在BC上，此时a=.

∴ <a<