题目内容
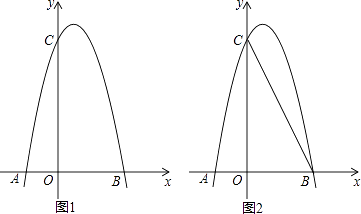
【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣5),C(6,0)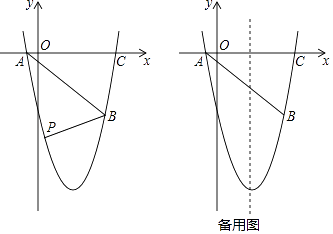
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)若点Q为抛物线的对称轴上的一个动点,试指出使△QAB为等腰三角形的点Q一共有几个?并请你求出其中一个点Q的坐标.
【答案】
(1)解:设y=a(x+1)(x﹣6)(a≠0),
把B(5,﹣5)代入:a(5+1)(5﹣6)=﹣5,
a= ![]() ,
,
∴y= ![]() (x+1)(x﹣6)=
(x+1)(x﹣6)= ![]() x2﹣
x2﹣ ![]() x﹣5
x﹣5
(2)解:存在,
如图1
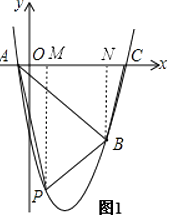
分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,
设P(m, ![]() m2﹣
m2﹣ ![]() m﹣5),四边形PACB的面积为S,
m﹣5),四边形PACB的面积为S,
则PM=﹣ ![]() m2+
m2+ ![]() m+5,AM=m+1,MN=5﹣m,CN=6﹣5=1,BN=5,
m+5,AM=m+1,MN=5﹣m,CN=6﹣5=1,BN=5,
∴S=S△AMP+S梯形PMNB+S△BNC,
= ![]() (﹣
(﹣ ![]() m2+
m2+ ![]() m+5)(m+1)+
m+5)(m+1)+ ![]() (5﹣
(5﹣ ![]() m2+
m2+ ![]() m+5)(5﹣m)+
m+5)(5﹣m)+ ![]() ×1×6,
×1×6,
=﹣ ![]() (m2﹣4m+4)+
(m2﹣4m+4)+ ![]()
=﹣ ![]() (m﹣2)2+
(m﹣2)2+ ![]() ,
,
当m=2时,S有最大值为 ![]() ,这时
,这时 ![]() m2﹣
m2﹣ ![]() m﹣5=
m﹣5= ![]() ×22﹣
×22﹣ ![]() ×2﹣5=﹣10,
×2﹣5=﹣10,
∴P(2,﹣10)
(3)解:这样的Q点一共有5个,
①以A为圆心,以AB为半径画弧,交抛物线的对称轴于Q1、Q4,则AQ1=AQ4=AB,
设对称轴交x轴于E,
y= ![]() x2﹣
x2﹣ ![]() x﹣5=
x﹣5= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ;
;
∴抛物线的对称轴是:x= ![]() ,
,
∵A(﹣1,0),B(5,﹣5),
∴AB= ![]() =
= ![]() ,
,
∴AE= ![]() +1=
+1= ![]() ,
,
由勾股定理得:Q1E=Q4E= ![]() =
= ![]() ,
,
∴Q1( ![]() ,
, ![]() ),Q4(
),Q4( ![]() ,﹣
,﹣ ![]() )
)
②

以B为圆心,以AB为半径画弧,交抛物线的对称轴于Q2、Q5,
∴Q2F=Q5F=AB= ![]() ,
,
过B作BF⊥Q1Q5于F,则Q2F=Q5F,
∵B(5,﹣5),
∴BF= ![]() ,
,
由勾股定理得:Q2F= ![]() =
= ![]() ,
,
∴Q5E= ![]() +5=
+5= ![]() ,
,
∴Q5( ![]() ,﹣
,﹣ ![]() ),
),
∵Q2E= ![]() ﹣5=
﹣5= ![]() ,
,
∴Q2( ![]() ,
, ![]() ),
),
③连接Q3A、Q3B,
因为Q3在对称轴上,所以设Q3( ![]() ,y),
,y),
∵△Q3AB是等腰三角形,且Q3A=Q3B,
由勾股定理得:( ![]() +1)2+y2=(
+1)2+y2=( ![]() ﹣5)2+(y+5)2,
﹣5)2+(y+5)2,
y=﹣ ![]() ,
,
∴Q3( ![]() ,﹣
,﹣ ![]() ).
).
综上所述,点Q的坐标为:Q1( ![]() ,
, ![]() ),Q2(
),Q2( ![]() ,
, ![]() ),Q3(
),Q3( ![]() ,﹣
,﹣ ![]() ).Q4(
).Q4( ![]() ,﹣
,﹣ ![]() )Q5(
)Q5( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)抛物线经过点A(﹣1,0),B(5,﹣5),C(6,0),可利用两点式法设抛物线的解析式为y=a(x+1)(x﹣6),代入B(5,﹣5)即可求得函数的解析式;(2)作辅助线,将四边形PACB分成三个图形,两个三角形和一个梯形,设P(m, ![]() m2﹣
m2﹣ ![]() m﹣5),四边形PACB的面积为S,用字母m表示出四边形PACB的面积S,发现是一个二次函数,利用顶点坐标求极值,从而求出点P的坐标.(3)分三种情况画图:①以A为圆心,AB为半径画弧,交对称轴于Q1和Q4,有两个符合条件的Q1和Q4;②以B为圆心,以BA为半径画弧,也有两个符合条件的Q2和Q5;③作AB的垂直平分线交对称轴于一点Q3,有一个符合条件的Q3;最后利用等腰三角形的腰相等,利用勾股定理列方程求出Q3坐标.
m﹣5),四边形PACB的面积为S,用字母m表示出四边形PACB的面积S,发现是一个二次函数,利用顶点坐标求极值,从而求出点P的坐标.(3)分三种情况画图:①以A为圆心,AB为半径画弧,交对称轴于Q1和Q4,有两个符合条件的Q1和Q4;②以B为圆心,以BA为半径画弧,也有两个符合条件的Q2和Q5;③作AB的垂直平分线交对称轴于一点Q3,有一个符合条件的Q3;最后利用等腰三角形的腰相等,利用勾股定理列方程求出Q3坐标.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?