题目内容
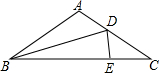
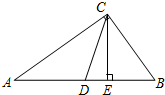
已知AE、AD分别是△ABC的高和角平分线，且∠B=46°，∠C=60°，求∠DAE的度数．
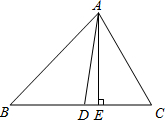
在△ABC中，∠B=46°，∠C=60°
∴∠BAC=180°-∠B-∠C=180°-46°-60°=74°
∵AD是的角平分线
∴∠DAC=
∠BAC=37°
∵AE是△ABC的高
∴∠AEC=90°
∴在△AEC中，∠EAC=180°-∠AEC-∠C=180°-90°-60°=30°
∴∠DAE=∠DAC-∠EAC=37°-30°=7°．
∴∠BAC=180°-∠B-∠C=180°-46°-60°=74°
∵AD是的角平分线
∴∠DAC=
| 1 |
| 2 |
∵AE是△ABC的高
∴∠AEC=90°
∴在△AEC中，∠EAC=180°-∠AEC-∠C=180°-90°-60°=30°
∴∠DAE=∠DAC-∠EAC=37°-30°=7°．
练习册系列答案
名校课堂系列答案
相关题目
