题目内容
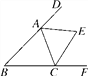
【题目】如图，∠B＝46°，△ABC的外角∠DAC和∠ACF的平分线交于点E，则∠AEC的度数为________．
【答案】67°
【解析】根据三角形内角和定理、角平分线的定义以及三角形外角定理求得:
∠DAC+∠ACF=（∠B+∠B+∠1+∠2）=113°；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数．
如图：
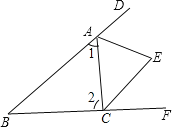
∵三角形的外角∠DAC和∠ACF的平分线交于点E，
∴∠EAC=∠DAC,∠ECA=∠ACF，
∵∠DAC=∠B+∠2，∠ACF=∠B+∠1.
∴∠DAC+∠ACF= (∠B+∠2)+ (∠B+∠1)= (∠B+∠B+∠1+∠2)，
∵∠B=46°(已知),∠B+∠1+∠2=180°(三角形内角和定理)，
∴∠DAC+∠ACF=113°.
∴∠AEC=180°(∠DAC+∠ACF)=67°.
故答案是：67°.
练习册系列答案
相关题目
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐重______千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价
元，则出售这20筐白菜可卖多少元？
