题目内容
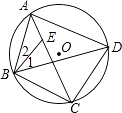
【题目】如图,在半径为50的⊙O中,弦AB的长为50, 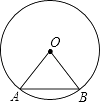
(1)求∠AOB的度数;
(2)求点O到AB的距离.
【答案】
(1)解:∵OA=OB=50,AB=50,
∴△OAB是等边三角形,
∴∠AOB=60°;
(2)解:过点O作OC⊥AB于点C,
则AC=BC= ![]() AB=25,
AB=25,
在Rt△OAC中,OC= ![]() =25
=25 ![]() .
.
即点O到AB的距离为25 ![]() .
.
【解析】(1)判断出三角形OAB是等边三角形即可得出∠AOB的度数;(2)过点O作OC⊥AB于点C,根据等边三角形的性质及勾股定理的知识,可求出OC.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目