Question

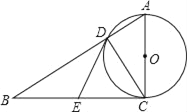
【题目】如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于E．则结论：①BE=EC；②∠EDC=∠ECD；③∠B=∠BDE；④△ABC∽△ACD；⑤△DEC是等边三角形．其中正确的结论有（　　）

A. 2个 B. 3个 C. 4个 D. 5个

Answer 1

【答案】C

【解析】分析：连接OD，如图，先判断BC为⊙O的切线，再利用切线长定理得到ED=EC，则∠1=∠2，接着证明∠3=∠B得到ED=EB，从而得到EB=EC，即可判断①②③；根据相似三角形的判定即可判断④；根据等边三角形的判定即可判断⑤．

详解：连接OD，如图，

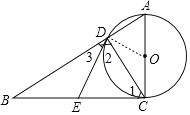
∵∠ACB=90°，

∴BC为⊙O的切线，

∵DE为切线，

∴ED=EC，

∴∠1=∠2，即∠EDC=∠ECD，∴②正确；

∵AC为直径，

∴∠ADC=90°，

∴∠2+∠3=90°，∠B+∠1=90°，

∴∠3=∠B，即∠B=∠BDE，∴③正确；

∴ED=EB，

∴EB=EC，∴①正确；

即点E是边BC的中点，

∵AC为直径，

∴∠ADC=90°=∠ACD，

∵∠A=∠A，

∴△ABC∽△ACD，∴④正确；

根据已知不能推出DC=DE=EC，即△DEC不一定是等边三角形，∴⑤错误；

即正确的个数是4个，

故选：C．