��Ŀ����
����Ŀ������������У�������ʦ�����ȡ�˾��꼶�ס������ಿ��ѧ������ij������Ŀ�IJ��ԣ����Գɼ�����ͳ�Ʒ�����������Ƶ���ֲ�����������ݱ��е���Ϣ����������⣺
��1��Ƶ���ֲ�����a=�� ����b=�� ����
��2�������У���꼶����ѧ��900�ˣ����Ƹ�У��������Ŀ�ijɼ�Ϊ�����ŵ�ѧ���ж����ˣ�
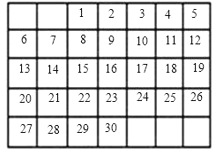
��3����֪��һ�����������װ�ѧ�����ڶ�����ֻ��һ���Ұ�ѧ������ʦ��������������и�ѡһ��ѧ�����������������飬����ѡ���������Ǽװ���Ұ��һ�˵ĸ����Ƕ��٣�
�֡����� | Ƶ�� | Ƶ�� |
��һ�飨������ | 3 | 0.15 |
�ڶ��飨�У� | b | 0.20 |
�����飨���� | 7 | 0.35 |
�����飨�ţ� | 6 | a |
���𰸡���1��0.3��4����2��585�ˣ���3��![]()
�������������������1���ɸ���֮��Ϊ1�ó�a��ֵ�����ݵ�һ��Ƶ����Ƶ�ʵó����������ٳ��Եڶ���Ƶ�ʿɵ�b��ֵ��
��2�����������������е���������Ƶ��֮�Ϳɵ���
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ������ѡ���������Ǽװ���Ұ��һ�˵�����������ø��ʹ�ʽ������ô𰸣�
���������������1��a=1����0.15+0.20+0.35��=0.3����������Ϊ��3��0.15=20���ˣ�����b=20��0.20=4���ˣ����ʴ�Ϊ��0.3��4��
��2��900����0.35+0.3��=585���ˣ���
�������Ƹ�У��������Ŀ�ijɼ�Ϊ�����ŵ�ѧ����585����
��3������״ͼ������
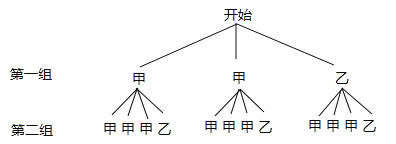
����״ͼ��֪����12�ֵȿ��ܽ����������ѡ���������Ǽװ���Ұ��һ�˵���5����������ѡ���������Ǽװ���Ұ��һ�˵ĸ���Ϊ![]() ��
��