Question

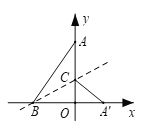
【题目】如图，在平面直角坐标系中，点A（0，b），点B（a，0），点D（-2，0），其中a、b满足， DE⊥x轴，且∠BED=∠ABO，直线AE交x轴于点C.

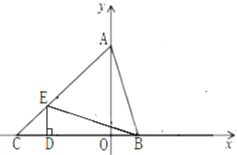
⑴ 分别求出点A、B的坐标；

⑵ 求证：△AOB≌△BDE，并求出点E的坐标

⑶ 若以AB为腰在第一象限内构造等腰直角△ABF，直接写出点F的坐标．

Answer 1

【答案】⑴ 点A（0，3）；点B（1，0）；⑵见解析，E（-2，1）；⑶（3，4）或（4，1）

【解析】

（1）根据算术平方根的非负性和绝对值的非负性，即可求出a、b，从而求出点A、B的坐标；

（2）根据点A的坐标为（0，3），点B的坐标为（1，0），点D的坐标为（-2，0），即可求出OA、OB、OD的长，从而证出OA= DB，再利用AAS即可证出：△AOB≌△BDE，从而得到OB=DE=1，最后即可求出E点坐标；

（3）根据等腰直角三角形腰的情况分类讨论：①若AB=AF，且∠BAF=90°时，过点F作FG⊥y轴于G，利用AAS证出△AOB≌△FGA，从而得到OB=GA=1，AO=FG=3，即可求出GO，从而求出F点坐标；②若AB=BF，且∠ABF=90°时，过点F作FG⊥x轴于G，原理同上.

解：（1）∵

∴

解得：

∴点A的坐标为（0，3），点B的坐标为（1，0）；

（2） ∵点A的坐标为（0，3），点B的坐标为（1，0），点D的坐标为（-2，0）

∴OA=3，OB=1，OD=2

∴DB= OD+ OB=3

∴OA= DB

在△AOB和△BDE中

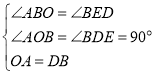
∴△AOB≌△BDE

∴OB=DE=1

∵E点在第二象限

∴点E坐标为（-2，1）

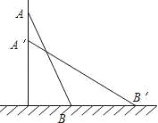
（3） ①若AB=AF，且∠BAF=90°时，过点F作FG⊥y轴于G，如下图所示

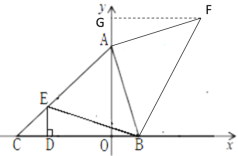
∴∠GAF＋∠OAB=90°，∠GAF＋∠GFA =90°

∴∠OAB=∠GFA

在△AOB和△FGA中

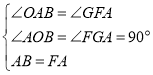
∴△AOB≌△FGA

∴OB=GA=1，AO=FG=3

∴GO= GA+ AO=4

此时点F的坐标为：（3，4）；

②若AB=BF，且∠ABF=90°时，过点F作FG⊥x轴于G

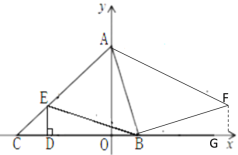
同理可证：△AOB≌△BGF

∴OB=GF=1，AO=BG=3

∴OG=OB+BG=4

此时点F的坐标为：（4，1）

综上所述：点F的坐标为（3，4）或（4，1）