题目内容
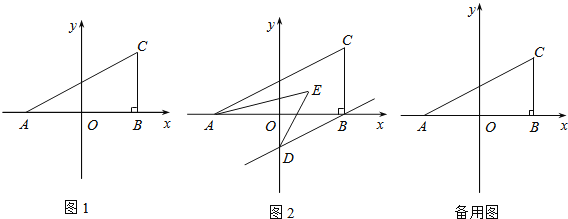
【题目】如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE= ![]() .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 .
.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 . 
【答案】![]() 或
或 ![]()
【解析】解:由tan∠AOE= ![]() ,可设A、B点坐标分别为(2m,3m)、(2n,3n),
,可设A、B点坐标分别为(2m,3m)、(2n,3n),
∵AD∥OC,
∴∠ADB=∠OCB,∠DAB=∠COA,
∴△BAD∽△BOC.
①当点A在第一象限时,如图1所示.
∵OC=2AD,
∴D点为线段BC的平分线,
∵C(0,c),B(2n,3n),
∴D点横坐标为 ![]() =n,
=n,
由题意知A、D点均在抛物线的对称轴上,
∴n=2m,
∴B点坐标为(4m,6m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有  ,
,
解得 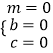 ,或
,或  ,
,
∵c>0,
∴c= ![]() ;
;
②当点A在第四象限时,如图2所示.
∵OC=2AD,
∴B点为线段CD的三等分点,
∵C(0,c),B(2n,3n),
∴D点横坐标为2n× ![]() =3n,
=3n,
由题意知A、D点均在抛物线的对称轴上,
∴3n=2m,
∴B点坐标为( ![]() m,2m),
m,2m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有 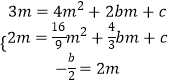 ,
,
解得 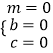 ,或
,或 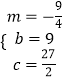 ,
,
∵c>0,
∴c= ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
相关题目