题目内容
【题目】如图①,正方形ABCD中,点A,B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D→A匀速运动,同时动点Q以相同的速度在x轴正半轴上运动,当点P到达A点时,两点同时停止运动,设运动的时间为t秒.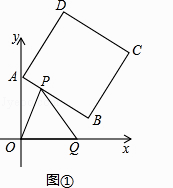
(1)当P点在边AB上运动时点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;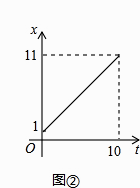
(2)求正方形边长及顶点C的坐标;
(3)在(1)中,设△OPQ的面积为S,求S与t的函数关系式并写出自变量的取值范围.
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等?若能,写出所有符合条件的t的值;若不能,请说明理由.
【答案】
(1)
解:如图①,过B作BF⊥OA于F,

∵A(0,10),
∴OA=10,
∵B(8,4),
∴BF=8,OF=4,
∴AF=10﹣4=6,
∴AB=10,
由图②知:点P在边AB上运动时间为10秒,所以速度为:10÷10=1,
Q(1,0),
则点P运动速度为每秒1个单位长度;
(2)
解:如图③,过B作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4,

由(1)知:AF=6,AB=10;
过C作CG⊥x轴于点G,与FB的延长线交于点H,
∵∠ABC=90°,AB=BC,
∴△ABF≌△BCH,
∴BH=AF=6,CH=BF=8,
∴OG=FH=8+6=14,CG=8+4=12,
∴所求C点的坐标为(14,12);
(3)
解:过点P作PM⊥y轴于点M,PN⊥x轴于点N,

∴PM∥BF,
则△APM∽△ABF,
∴ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AM= ![]() ,PM=
,PM= ![]() t,
t,
∴PN=OM=10﹣ ![]() t,ON=PM=
t,ON=PM= ![]() t,
t,
∴S=S△OPQ= ![]() PNOQ
PNOQ
= ![]() ×(10﹣
×(10﹣ ![]() t)(1+t)=﹣
t)(1+t)=﹣ ![]() (0≤t≤10);
(0≤t≤10);
(4)
解:OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半时,满足条件;
①当P在AB上时,如图③, ![]() t=
t= ![]() (t+1),t=
(t+1),t= ![]() ,OP与PQ相等,
,OP与PQ相等,

②当P在BC上时,如图④,则PB=t﹣10,

sin∠ABF=sin∠BPM= ![]() ,
,
∴ ![]() ,
,
∴BM= ![]() (t﹣10),
(t﹣10),
∴ON=BF+BM=8+ ![]() (t﹣10),
(t﹣10),
8+ ![]() (t﹣10)=
(t﹣10)= ![]() (t+1),解得:t=﹣15(舍),
(t+1),解得:t=﹣15(舍),
③当P在CD上时,如图⑤,则PC=t﹣20,
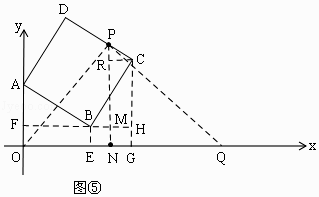
cos∠PCR=cos∠BCH= ![]() ,
,
∴ ![]() ,
,
∴CR=MH= ![]() (t﹣20),
(t﹣20),
∴ON=OG﹣NG=FH﹣MH=14﹣ ![]() (t﹣20),
(t﹣20),
14﹣ ![]() (t﹣20)=
(t﹣20)= ![]() (t+1),解得:t=
(t+1),解得:t= ![]() ,
,
即当t= ![]() 时,OP=PQ,
时,OP=PQ,
综上所述,当t= ![]() 或
或 ![]() 时,OP与PQ相等.
时,OP与PQ相等.
【解析】(1)由A和B两点的坐标求正方形边长AB,由图②得:P在边AB上运动10秒,Q开始运动时,横坐标为1;(2)由(1)知,正方形边长为10,根据三角形全等得:BH=AF=6,CH=BF=8,所以可得OG=14,CG=12,写出C点的坐标;(3)作辅助线,证明△APM∽△ABF,列比例式得:AM= ![]() ,PM=
,PM= ![]() t,根据面积公式可得S与t的关系式;(4)OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半;分三种情况进行讨论:点P分别在AB、BC、CD上时,根据这一等量关系列式可得t的值.
t,根据面积公式可得S与t的关系式;(4)OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半;分三种情况进行讨论:点P分别在AB、BC、CD上时,根据这一等量关系列式可得t的值.

 阅读快车系列答案
阅读快车系列答案