题目内容
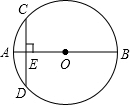
已知:如图,圆内接四边形ABCD的两边AB、DC的延长线相交于点E,DF过圆心O交AB于点F,AB=BE,连接AC,且OD=3,AF=FB=
,求AC的长.

| 5 |

连接OA,
∵DF过点O,AF=FB=
,
∴∠AFO=90°.
∴FO=
=
=2.
∴DF=DO+FO=5.
∴AD=
=
.
DE=
=
.
由垂径定理知
=
,
∴∠DCA=∠DAB.
∵∠ADC是△ADC与△EDA的公共角,
∴△ADC∽△EDA.
∴
=
,
=
.
∴AC=
.

∵DF过点O,AF=FB=
| 5 |
∴∠AFO=90°.
∴FO=
| AO2-AF2 |
| 9-5 |
∴DF=DO+FO=5.
∴AD=
| AF2+DF2 |
| 30 |
DE=
| FE2+DF2 |
| 70 |
由垂径定理知
 |
| AD |
 |
| DB |
∴∠DCA=∠DAB.
∵∠ADC是△ADC与△EDA的公共角,
∴△ADC∽△EDA.
∴
| AC |
| AE |
| AD |
| DE |
| AC | ||
4
|
| ||
|
∴AC=
4
| ||
| 7 |


练习册系列答案
相关题目