题目内容
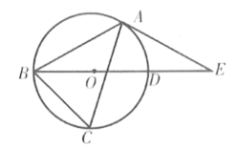
【题目】如图,圆![]() 是
是![]() 的外接圆,其切线
的外接圆,其切线![]() 与直径
与直径![]() 的延长线相交于点
的延长线相交于点![]() ,且
,且![]() .
.
(1)求![]() 的度数;
的度数;
(2)若![]() ,求圆
,求圆![]() 的半径.
的半径.
【答案】(1)![]() 的度数为
的度数为![]() ;(2)圆O的半径为2.
;(2)圆O的半径为2.
【解析】
(1)如图(见解析),设![]() ,先根据等腰三角形的性质得出
,先根据等腰三角形的性质得出![]() ,再根据圆的性质可得
,再根据圆的性质可得![]() ,从而可得
,从而可得![]() ,然后根据圆的切线的性质可得
,然后根据圆的切线的性质可得![]() ,又根据三角形的内角和定理可求出x的值,从而可得
,又根据三角形的内角和定理可求出x的值,从而可得![]() 的度数,最后根据圆周角定理即可得;
的度数,最后根据圆周角定理即可得;
(2)如图(见解析),设圆O的半径为![]() ,先根据圆周角定理得出
,先根据圆周角定理得出![]() ,再根据直角三角形的性质可得
,再根据直角三角形的性质可得![]() ,从而可得
,从而可得![]() ,然后在
,然后在![]() 中,利用勾股定理求解即可得.
中,利用勾股定理求解即可得.
(1)如图,连接OA
设![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() AE是圆O的切线
AE是圆O的切线
![]() ,即
,即![]()
![]()
在![]() 中,由三角形的内角和定理得:
中,由三角形的内角和定理得:![]()
即![]()
解得![]()
![]()
则由圆周角定理得:![]()
故![]() 的度数为
的度数为![]() ;
;
(2)如图,连接AD
设圆O的半径为![]() ,则
,则![]()
![]()
![]()
![]() BD是圆O的直径
BD是圆O的直径
![]()
由(1)可知,![]()
则在![]() 中,
中,![]()
![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
则圆O的半径为2.


练习册系列答案
相关题目
【题目】2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数![]() (人)与时间
(人)与时间![]() (分钟)的变化情况,数据如下表:(表中9-15表示
(分钟)的变化情况,数据如下表:(表中9-15表示![]() )
)
时间 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
人数 | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?