题目内容
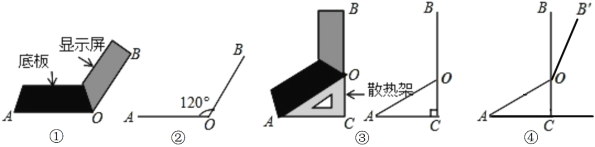
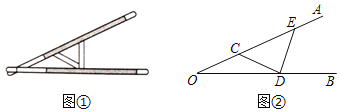
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有糟的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠AOB是______°.
【答案】28
【解析】
根据OC=CD=DE,可得∠O=∠ODC,∠DCE=∠DEC,根据三角形的外角性质可知∠DCE=∠O+∠ODC=2∠ODC,进一步根据三角形的外角性质可知∠BDE=3∠ODC=84°,即可求出∠ODC的度数,则可求出∠AOB的度数.
∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=84°,
∴∠ODC=28°,
∴∠O=28°,
即∠AOB=28°.
故答案为:28.

练习册系列答案
相关题目