ЬтФПФкШн
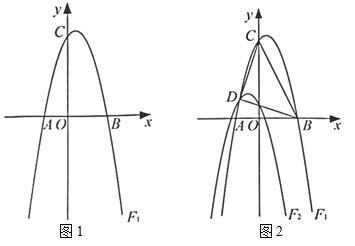
ЁОЬтФПЁПвбжЊЃКЖўДЮКЏЪ§y=x2+2mx+2nЃЌНЛxжсгкA,BСНЕу(AдкBЕФзѓВр)
ЃЈ1ЃЉЕБm=3ЪБЃЌn=4ЪБЃЌ ЂйЧѓAЁЂBСНЕузјБъЃЛЂкНЋХзЮяЯпЯђгвЦНвЦkИіЕЅЮЛКѓНЛxжсгкMЁЂNЃЈMдкNЕФзѓВрЃЉЃЌШєBЁЂMШ§ЕШЗжANЃЌжБНгаДГіkЕФжЕЃЛ
ЃЈ2ЃЉЕБm=1ЪБЃЌШєЯпЖЮABЩЯгаЧвжЛга5ИіЕуЕФКсзјБъЮЊећЪ§ЃЌЧѓnЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉМЧA(x1,0)ЁЂB(x2,0)ЃЌЕБmЁЂnЖМЪЧЦцЪ§ЪБЃЌx1ЁЂx2ФмЗёЪЧгаРэЪ§ЃПШєФмЃЌЧыОйР§бщжЄЃЌШєВЛФмЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁП(1)Ђй (-4,0)ЃЛ(-2,0)ЃЛЂк 1 ЃЛ (2)-4ЃМnЃМ![]() ЃЛ(3)МћНтЮі
ЃЛ(3)МћНтЮі
ЁОНтЮіЁП
(1)ЂйЕБm=3ЪБЃЌn=4ЪБЃЌЖўДЮКЏЪ§НтЮіЪНЮЊy=x2+6x+8ЃЌСюy=0ЃЌНтЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЂкИљОнЬѕМўЧѓГіЕуMЕФзјБъМДПЩНтОіЮЪЬтЃЎ
(2)гЩЬтвтПЩжЊЃЌx=1ЪБЃЌyЃМ0ЃЛx=2ЪБЃЌyЃО0ЃЛСаГіВЛЕШЪНМДПЩНтОіЮЪЬтЃЎ
(3)ЕБmЁЂnЖМЪЧЦцЪ§ЪБЃЌx1ЁЂx2ВЛПЩФмЪЧгаРэЪ§ЃЎгУЗДжЄЗЈжЄУїМДПЩЃЎ
НтЃКЃЈ1ЃЉЕБmЃН3ЪБЃЌnЃН4ЪБЃЌЖўДЮКЏЪ§НтЮіЪНЮЊyЃНx2+6x+8ЃЌ
ЂйСюyЃН0ЕУЕНx2+6x+8ЃН0ЃЌНтЕУxЃНЉ2ЛђЉ4ЃЌЁрAЃЈЉ4ЃЌ0ЃЉЃЌBЃЈЉ2ЃЌ0ЃЉЃЎ
ЙЪД№АИЮЊЃКA(-4,0),B(-2,0).
ЂкЁпХзЮяЯпЯђгвЦНвЦkИіЕЅЮЛКѓНЛxжсгкMЁЂNЃЈMдкNЕФзѓВрЃЉЃЌ
BЁЂMШ§ЕШЗжANЃЌABЃН2ЃЌ
ЁрAMЃНBMЃН1ЃЌ
ЁрMЃЈЉ3ЃЌ0ЃЉЃЌМДkЃН1ЃЎ
ЙЪД№АИЮЊЃКk=1.
ЃЈ2ЃЉЁпmЃН1ЪБЃЌХзЮяЯпЕФЖдГЦжсxЃНЉ1ЃЌ
ЁрЯпЖЮABЩЯгаЧвжЛга5ИіЕуЕФКсзјБъЮЊећЪ§ЃЌетаЉећЪ§ЮЊЉ3ЃЌЉ2ЃЌЉ1ЃЌ0ЃЌ1ЃЌ
ЁрxЃН1ЪБЃЌyЃМ0ЃЛxЃН2ЪБЃЌyЃО0ЃЛ
Ёр![]() ЃЌНтЕУЃК-4ЃМnЃМ
ЃЌНтЕУЃК-4ЃМnЃМ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК-4ЃМnЃМ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЕБmЁЂnЖМЪЧЦцЪ§ЪБЃЌx1ЁЂx2ВЛПЩФмЪЧгаРэЪ§ЃЎ
РэгЩЃКМйЩшmЁЂnЖМЪЧЦцЪ§ЪБЃЌx1ЁЂx2ЪЧгаРэЪ§ЃЌ
Ёпx1x2ЃН2nЃЌ
Ёрx1ЃЌx2жаПЯЖЈвЛИіЪЧЦцЪ§ЃЌвЛИіЪЧХМЪ§ЃЌ
Ёрx1+x2вЛЖЈЪЧЦцЪ§ЃЌгЩЬтвтx1+x2=-2mЪЧХМЪ§ЃЌгыМйЩшУЌЖмЃЌ
ЁрМйЩшВЛГЩСЂЃЌ
ЁрЕБmЁЂnЖМЪЧЦцЪ§ЪБЃЌx1ЁЂx2ВЛПЩФмЪЧгаРэЪ§ЃЎ
ЙЪД№АИЮЊЃКЕБmЁЂnЖМЪЧЦцЪ§ЪБЃЌx1ЁЂx2ВЛПЩФмЪЧгаРэЪ§ЃЎ

 ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ МйЦкзївЕЪюМйГЩГЄРждАаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
МйЦкзївЕЪюМйГЩГЄРждАаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИЁОЬтФПЁП2020ФъЬхг§жаПМЃЌдіЩшСЫПМЩњНјШыПМЕуашНјааЬхЮТМьВтЕФвЊЧѓЃЎЗРвпВПУХЮЊСЫНтбЇЩњДэЗхНјШыПМЕуНјааЬхЮТМьВтЕФЧщПіЃЌЕїВщСЫвЛЫљбЇаЃФГЬьЩЯЮчПМЩњНјШыПМЕуЕФРлМЦШЫЪ§![]() ЃЈШЫЃЉгыЪБМф
ЃЈШЫЃЉгыЪБМф![]() ЃЈЗжжгЃЉЕФБфЛЏЧщПіЃЌЪ§ОнШчЯТБэЃКЃЈБэжа9-15БэЪО
ЃЈЗжжгЃЉЕФБфЛЏЧщПіЃЌЪ§ОнШчЯТБэЃКЃЈБэжа9-15БэЪО![]() ЃЉ
ЃЉ
ЪБМф | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
ШЫЪ§ | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
ЃЈ1ЃЉИљОнет15ЗжжгФкПМЩњНјШыПМЕуЕФРлМЦШЫЪ§гыЪБМфЕФБфЛЏЙцТЩЃЌРћгУГѕжаЫљбЇКЏЪ§жЊЪЖЧѓГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШчЙћПМЩњвЛНјПМЕуОЭПЊЪМВтСПЬхЮТЃЌЬхЮТМьВтЕуга2ИіЃЌУПИіМьВтЕуУПЗжжгМьВт20ШЫЃЌПМЩњХХЖгВтСПЬхЮТЃЌЧѓХХЖгШЫЪ§зюЖрЪБгаЖрЩйШЫЃПШЋВППМЩњЖМЭъГЩЬхЮТМьВташвЊЖрЩйЪБМфЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЙћвЊдк12ЗжжгФкШУШЋВППМЩњЭъГЩЬхЮТМьВтЃЌДгвЛПЊЪМОЭгІИУжСЩйдіМгМИИіМьВтЕуЃП
ЁОЬтФПЁПОХФъМЖвЛАрбћЧы![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮхЮЛЦРЮЏЖдМзЁЂввСНЮЛЭЌбЇЕФВХвеБэбнДђЗжЃЌВЂзщжЏШЋАр50УћЭЌбЇЖдСНШЫУёвтВтЦРЭЖЦБЃЌЛцжЦСЫШчЯТЕФДђЗжБэКЭВЛЭъећЕФЬѕаЮЭГМЦЭМЃК
ЮхЮЛЦРЮЏЖдМзЁЂввСНЮЛЭЌбЇЕФВХвеБэбнДђЗжЃЌВЂзщжЏШЋАр50УћЭЌбЇЖдСНШЫУёвтВтЦРЭЖЦБЃЌЛцжЦСЫШчЯТЕФДђЗжБэКЭВЛЭъећЕФЬѕаЮЭГМЦЭМЃК
ЮхЮЛЦРЮЏЕФДђЗжБэ
A | B | C | D | E | |
Мз | 89 | 91 | 93 | 94 | 86 |
вв | 88 | 87 | 90 | 98 | 92 |
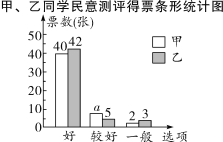
ВЂЧѓЕУСЫЮхЮЛЦРЮЏЖдМзЭЌбЇВХвеБэбнЫљДђЗжЪ§ЕФЦНОљЗжКЭжаЮЛЪ§ЃК
![]() ЃЈЗжЃЉЃЛжаЮЛЪ§ЪЧ91Зж.
ЃЈЗжЃЉЃЛжаЮЛЪ§ЪЧ91Зж.
ЃЈ1ЃЉЧѓЮхЮЛЦРЮЏЖдввЭЌбЇВХвеБэбнЫљДђЗжЪ§ЕФЦНОљЗжКЭжаЮЛЪ§ЃЛ
ЃЈ2ЃЉ![]() ________ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
________ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЮЊСЫДгМзЁЂввСНШЫжажЛбЁАЮГівЛШЫШЅВЮМгвеЪѕНкбнГіЃЌАрМЖжЦЖЈСЫШчЯТЕФбЁАЮЙцдђЃК
бЁАЮЙцдђЃКбЁАЮзлКЯЗжзюИпЕФЭЌбЇВЮМгвеЪѕНкбнГі.ЦфжаЃЌзлКЯЗжЃНВХвеЗж![]() ВтЦРЗж
ВтЦРЗж![]() ЃЛ
ЃЛ
ВХвеЗжЃНЮхЮЛЦРЮЏЫљДђЗжЪ§жаШЅЕєвЛИізюИпЗжКЭвЛИізюЕЭЗжЃЌдйЫуЦНОљЗжЃЛВтЦРЗжЃНЁАКУЁБЦБЪ§ЁС2ЗжЃЋЁАНЯКУЁБЦБЪ§ЁС1ЗжЃЋЁАвЛАуЁБЦБЪ§ЁС0Зж
ЂйЕБ![]() ЪБЃЌЭЈЙ§МЦЫуЫЕУїгІбЁАЮФФЮЛЭЌбЇШЅВЮМгвеЪѕНкбнГіЃП
ЪБЃЌЭЈЙ§МЦЫуЫЕУїгІбЁАЮФФЮЛЭЌбЇШЅВЮМгвеЪѕНкбнГіЃП
ЂкЭЈЙ§МЦЫуЫЕУї![]() ЕФжЕВЛФмЪЧЖрЩйЃП
ЕФжЕВЛФмЪЧЖрЩйЃП